
科目: 来源: 题型:
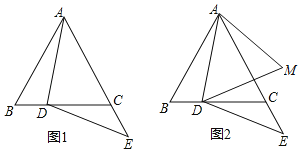
【题目】在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1).
(1)求证:∠BAD=∠EDC;
(2)若点E关于直线BC的对称点为M(如图2),连接DM,AM.求证:DA=AM.
查看答案和解析>>
科目: 来源: 题型:
【题目】某体育用品商店欲购进A、B两种品牌的足球进行销售,若购进A种品牌的足球50个,B种品牌的足球25个,需花费成本4250元;若购进A种品牌的足球15个,B种品牌的足球10个,需花费成本1450元.
(1)求购进A、B两种品牌的足球每个各需成本多少元;
(2)根据市场调研,A种品牌的足球每个售价90元,B种品牌的足球每个售价120元,该体育用品商店购进A、B两种品牌的足球进行销售,恰好用了7000元的成本.正值俄罗斯世界怀开赛,为了回馈新老顾客,决定A品牌足球按售价降低20元出售,B品牌足球按售价的7折出售,且保证利润不低于2000元,问A种品牌的足球至少购进多少个.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图抛物线y=ax2+bx+c的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:
①2b﹣c=2;②a= ![]() ;③ac=b﹣1;④
;③ac=b﹣1;④ ![]() >0
>0
其中正确的个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料:小明遇到这样一个问题;△ABC中,有两个内角相等.
①若∠A=110°,求∠B的度数;
②若∠A=40°,求∠B的度数.
小明通过探究发现,∠A的度数不同,∠B的度数的个数也可能不同,因此为同学们提供了如下解题的想法:
对于问题①,根据三角形内角和定理,∵∠A=110°>90°,∠B=∠C=35°;
对于问题②,根据三角形内角和定理,∵∠A=40°<90°,∴∠A=∠B或∠A=∠C或∠B=∠C,∴∠B的度数可求.请回答:
(1)问题②中∠B的度数为 ;
(2)参考小明解决问题的思路,解决下面问题:
△ABC中,有两个内角相等.设∠A=x°,当∠B有三个不同的度数时,求∠B的度数(用含x的代式表示)以及x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于二次函数y=x2﹣2mx﹣3,下列结论错误的是( )
A.它的图象与x轴有两个交点
B.方程x2﹣2mx=3的两根之积为﹣3
C.它的图象的对称轴在y轴的右侧
D.x<m时,y随x的增大而减小
查看答案和解析>>
科目: 来源: 题型:
【题目】共有1500kg化工原料,由A,B两种机器人同时搬运,其中,A型机器人比B型机器每小时多搬运30kg,A型机器人搬运900kg所用时间与B型机器人搬运600kg所用时间相等,问需要多长时间才能运完?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c的顶点为B(﹣1,3),与x轴的交点A在点(﹣3,0)和(﹣2,0)之间,以下结论:
①b2﹣4ac=0;②a+b+c>0;③2a﹣b=0;④c﹣a=3
其中正确的有( )个.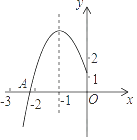
A.1
B.2
C.3
D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】有这样一个问题:探究同一平面直角坐标系中系数互为倒数的正、反比例函数y= ![]() x与y=
x与y= ![]() (k≠0)的图象性质.
(k≠0)的图象性质.
小明根据学习函数的经验,对函数y= ![]() x与y=
x与y= ![]() ,当k>0时的图象性质进行了探究.
,当k>0时的图象性质进行了探究.
下面是小明的探究过程: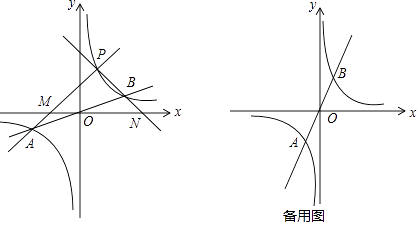
(1)如图所示,设函数y= ![]() x与y=
x与y= ![]() 图象的交点为A,B,已知A点的坐标为(﹣k,﹣1),则B点的坐标为;
图象的交点为A,B,已知A点的坐标为(﹣k,﹣1),则B点的坐标为;
(2)若点P为第一象限内双曲线上不同于点B的任意一点.
①设直线PA交x轴于点M,直线PB交x轴于点N.求证:PM=PN.
证明过程如下,设P(m, ![]() ),直线PA的解析式为y=ax+b(a≠0).
),直线PA的解析式为y=ax+b(a≠0).
则 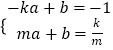 ,
,
解得 ![]()
∴直线PA的解析式为 ![]()
请你把上面的解答过程补充完整,并完成剩余的证明.
②当P点坐标为(1,k)(k≠1)时,判断△PAB的形状,并用k表示出△PAB的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的中线,E,F为直线AD上的点,连接BE,CF,且BE∥CF.
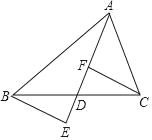
(1)求证:DE=DF;
(2)若在原有条件基础上再添加AB=AC,你还能得出什么结论.(不用证明)(写2个)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com