
科目: 来源: 题型:
【题目】阅读理(解析)
提出问题:如图1,在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间有什么关系?探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
当AP=![]() AD时(如图2):
AD时(如图2):
∵AP=![]() AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
∴S△ABP=![]() S△ABD,
S△ABD,
∵PD=AD﹣AP=![]() AD,△CDP和△CDA的高相等
AD,△CDP和△CDA的高相等
∴S△CDP=![]() S△CDA,
S△CDA,
∴S△PBC=S四边形ABCD﹣S△ABP﹣S△CDP=S四边形ABCD﹣![]() S△ABD﹣
S△ABD﹣![]() S△CDA,
S△CDA,
=S四边形ABCD﹣![]() (S四边形ABCD﹣S△DBC)﹣
(S四边形ABCD﹣S△DBC)﹣![]() (S四边形ABCD﹣S△ABC)=
(S四边形ABCD﹣S△ABC)=![]() S△DBC+
S△DBC+![]() S△ABC.
S△ABC.
(1)当AP=![]() AD时,探求S△PBC与S△ABC和S△DBC之间的关系式并证明;
AD时,探求S△PBC与S△ABC和S△DBC之间的关系式并证明;
(2)当AP=![]() AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
(3)一般地,当AP=![]() AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系为: ;
AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系为: ;
(4)当AP=![]() AD(0≤
AD(0≤![]() ≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .
≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .

查看答案和解析>>
科目: 来源: 题型:
【题目】某商厦进货员预测一种应季衬衫能畅销市场,就用![]() 万元购进这种衬衫,面市后果然供不应求.商厦又用
万元购进这种衬衫,面市后果然供不应求.商厦又用![]() 万元购进第二批这种衬衫,所购数量是第一批进量的
万元购进第二批这种衬衫,所购数量是第一批进量的![]() 倍,但单价贵了
倍,但单价贵了![]() 元.商厦销售这种衬衫时每件定价
元.商厦销售这种衬衫时每件定价![]() 元,最后剩下
元,最后剩下![]() 件按八折销售,很快售完.在这两笔生意中,商厦共盈利多少元?
件按八折销售,很快售完.在这两笔生意中,商厦共盈利多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低![]() 元.
元.
(1)填表:(不需化简)
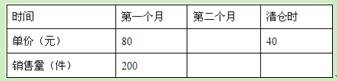
(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】点D是等边△ABC(即三条边都相等,三个角都相等的三角形)边BA上任意一点(点D与点B不重合),连接DC.
(1)如图1,以DC为边在BC上方作等边△DCF,连接AF,猜想线段AF与BD的数量关系?请说明理由.
(2)如图2,若以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF、BF′,探究AF、BF′与AB有何数量关系?请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】某市推行“节能减排,低碳经济”政策后,某环保节能设备生产企业的产品供不应求.若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于90万元.已知这种设备的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=170﹣2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
(1)直接写出y2与x之间的函数关系式;
(2)求月产量x的范围;
(3)当月产量x(套)为多少时,这种设备的利润为1950万元?

查看答案和解析>>
科目: 来源: 题型:
【题目】某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示.根据图象解答下列问题:

(1)洗衣机的进水时间是多少分钟?清洗时洗衣机中水量为多少升?
(2)已知洗衣机的排水速度为每分钟19升.
①求排水时洗衣机中的水量y(升)与时间x(分钟)与之间的关系式;
②如果排水时间为2分钟,求排水结束时洗衣机中剩下的水量.
查看答案和解析>>
科目: 来源: 题型:
【题目】计算
(1)(![]() )﹣2﹣(﹣2)0+(﹣0.2)2018×(﹣5)2018;
)﹣2﹣(﹣2)0+(﹣0.2)2018×(﹣5)2018;
(2)用整式乘法公式计算:1012﹣1;
(3)(x2y+2x2y﹣y3)÷y﹣(y+2x)(2x﹣y);
(4)先化简,再求值:(a﹣2b)2+(a﹣b)(a+b)﹣2(a﹣3b)(a﹣b),其中,a=1,b=﹣2.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两公司为“见义勇为基金会”各捐款3000元.已知甲公司的人数比乙公司的人数多20%,乙公司比甲公司人均多捐20元.请你根据上述信息,就这两个公司的“人数”或“人均捐款”提出一个用分式方程解决的题,并写出解题过程.
查看答案和解析>>
科目: 来源: 题型:
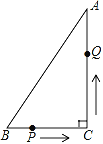
【题目】如图,在Rt△ABC中,AC=24cm,BC=7cm,P点在BC上,从B点到C点运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为5cm/s.若点P、Q分别从B、C同时运动,且运动时间记为t秒,请解答下面的问题,并写出探索的主要过程.
(1)当t为何值时,P、Q两点的距离为5![]() cm?
cm?
(2)当t为何值时,△PCQ的面积为15cm2?
(3)请用配方法说明,点P运动多少时间时,四边形BPQA的面积最小?最小面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com