
科目: 来源: 题型:
【题目】将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG.

(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;
(2)若AB=8,AD=4,求四边形DHBG的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )

A. ![]() B.
B. ![]() C. 3 D.
C. 3 D. ![]()
查看答案和解析>>
科目: 来源: 题型:
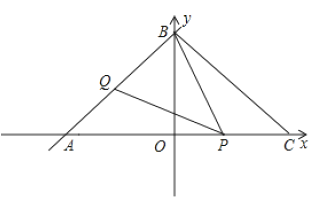
【题目】如图,一次函数![]() 的图象与
的图象与![]() ,
,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,点
两点,点![]() 与点
与点![]() 关于
关于![]() 轴对称.动点
轴对称.动点![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上(点
上(点![]() 与点
与点![]() ,
,![]() 不重合),且满足
不重合),且满足![]() .
.
(1)求点![]() ,
,![]() 的坐标及线段
的坐标及线段![]() 的长度;
的长度;
(2)当点![]() 在什么位置时,
在什么位置时,![]() ,说明理由;
,说明理由;
(3)当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是____________。

查看答案和解析>>
科目: 来源: 题型:
【题目】为了迎接2022年北京冬奥会,萍乡外国语学校组织了一次大型长跑比赛。甲,乙两人在比赛时,路程![]() (米)与时间
(米)与时间![]() (分钟)的关系如图所示,极据图像解答下列问题:
(分钟)的关系如图所示,极据图像解答下列问题:

(1)这次长跑比赛的全程是___米;先到达终点的人比另一个人领先____分钟:
(2)乙是学校田径队运动员,十分注意比赛技巧,比赛过程分起跑、途中跑冲刺跑三阶段,经历了两次加速过程.问第![]() 分钟时乙还落后甲多少米?
分钟时乙还落后甲多少米?
(3)假设乙在第一次加速后,始终保持这个速度继续前进。那么甲,乙两人谁先到达终点?请说明理由.
(4)事实上乙追上甲的时间是多少分钟?
查看答案和解析>>
科目: 来源: 题型:
【题目】材料阅读:如图①所示的图形,像我们常见的学习用品—圆规.我们不妨把这样图形叫做“规形图”.
解决问题:
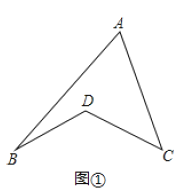
(1)观察“规形图”,试探究![]() 与
与![]() ,
,![]() ,
,![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(2)请你直接利用以上结论,解决以下两个问题:
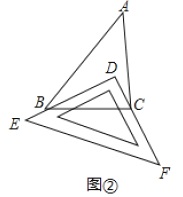
Ⅰ.如图②,把一块三角尺![]() 放置在
放置在![]() 上,使三角尺的两条直角边
上,使三角尺的两条直角边![]() ,
,![]() 恰好经过点
恰好经过点![]() ,
,![]() ,若
,若![]() ,则
,则![]() _____
_____![]() .
.
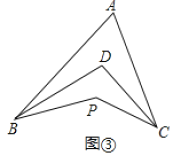
Ⅱ.如图③,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列四幅图象近似刻画两个变量之间的关系,请按图象顺序将下面四种情景与之对应排序( )

①一辆汽车在公路上匀速行驶(汽车行驶的路程与时间的关系)
②向锥形瓶中匀速注水(水面的高度与注水时间的关系)
③将常温下的温度计插入一杯热水中(温度计的读数与时间的关系)
④一杯越来越凉的水(水温与时间的关系)
A. ③②④①B. ③④②①C. ①④②③D. ①②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】某农场去年大豆和小麦的总产量为200吨,今年大豆和小麦的总产量为225吨,其中大豆比去年増产5%,小麦比去年増产15%,求该农场今年大豆和小麦的产量各是多少吨?
查看答案和解析>>
科目: 来源: 题型:
【题目】某同学在![]() ,
,![]() 两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是
两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是![]() 元,且随身听的单价比书包的单价的
元,且随身听的单价比书包的单价的![]() 倍少
倍少![]() 元.
元.
(1)求该同学看中的随身听和书包的单价各是多少元?
(2)某一天该同学上街,恰好赶上商家促销,超市![]() 所有商品打八五折销售,超市
所有商品打八五折销售,超市![]() 全场购物每满
全场购物每满![]() 元返购物券
元返购物券![]() 元销售(不足
元销售(不足![]() 元不返券,购物券全场通用),但他只带了
元不返券,购物券全场通用),但他只带了![]() 元钱,如果他只在一家超市购买看中的这两样商品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
元钱,如果他只在一家超市购买看中的这两样商品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
查看答案和解析>>
科目: 来源: 题型:
【题目】某批发市场经销龟苓膏粉,其中![]() 品牌的批发价是每包20元,
品牌的批发价是每包20元,![]() 品牌的批发价是每包25元,小明计划购买这两种品牌的龟苓膏粉共1000包,解答下列问题:
品牌的批发价是每包25元,小明计划购买这两种品牌的龟苓膏粉共1000包,解答下列问题:
(1)若购买这些龟苓膏粉共花费22000元,求两种品牌的龟苓膏粉各购买了多少包?
(2)若凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元,
若购买会员卡并用此卡购买这些龟苓膏粉共花费![]() 元,设
元,设![]() 品牌购买了
品牌购买了![]() 包,请求出
包,请求出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com