
科目: 来源: 题型:
【题目】为了预防流感,某学校在休息天用药薰消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与反比例函数![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
(1)试确定上述反比例函数和一次函数的表达式.
(2)求△AOB的面积.
(3)比较y1和y2的大小.

查看答案和解析>>
科目: 来源: 题型:
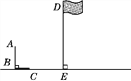
【题目】如图,九年级(1)班的小明与小艳两位同学去操场测量旗杆DE的高度,已知直立在地面上的竹竿AB的长为3 m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2 m.
(1)请你在图中画出此时旗杆DE在阳光下的投影,并写出画图步骤;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6 m,请你计算旗杆DE的高度.
查看答案和解析>>
科目: 来源: 题型:
【题目】下图是2019年5月17日至31日某市的空气质量指数趋势图.
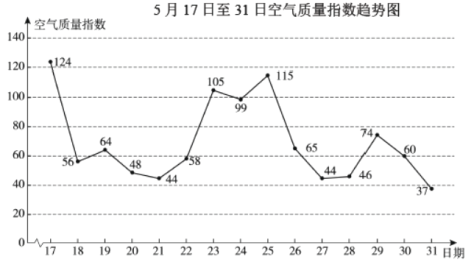
(说明:空气质量指数为0-50、51-100、101-150分别表示空气质量为优、良、轻度污染)
有如下结论:
①在此次统计中,空气质量为优的天数少于轻度污染的天数;
②在此次统计中,空气质量为优良的天数占![]() ;
;
③20,21,22三日的空气质量指数的方差小于26,27,28三日的空气质量指数的方差.
上述结论中,所有正确结论的序号是( )
A.①B.①③C.②③D.①②③
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,平面直角坐标系中,在边长为1的正方形![]() 的边上有—动点
的边上有—动点![]() 沿正方形运动一周,
沿正方形运动一周,![]() 则
则![]() 的纵坐标
的纵坐标![]() 与点
与点![]() 走过的路程
走过的路程![]() 之间的函数关系用图象表示大致是( )
之间的函数关系用图象表示大致是( )
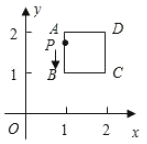
A. 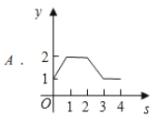 B.
B. 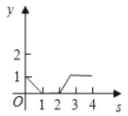 C.
C. 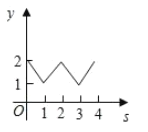 D.
D. 
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,平行四边形![]() 中,对角线
中,对角线![]() 的垂直平分线分别交
的垂直平分线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() 、
、![]() ;
;


(1)如图1,求证:四边形![]() 是菱形;
是菱形;
(2)如图2,当![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,使
,使![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
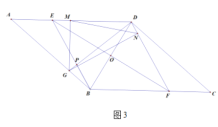
(3)如图3,在(2)的条件下,![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为![]() ,
,![]() ,
,![]() ,
,![]() ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为![]() .如图2第一行数字从左到右依次为0,1,0,1,序号为
.如图2第一行数字从左到右依次为0,1,0,1,序号为![]() ,表示该生为5班学生.表示6班学生的识别图案是( )
,表示该生为5班学生.表示6班学生的识别图案是( )


A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源: 题型:
【题目】(一)知识链接
若点M,N在数轴上,且M,N代表的实数分别是a,b,则线段MN的长度可表示为 .
(二)解决问题
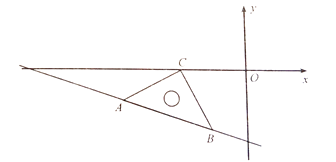
如图,将一个三角板放置在平面直角坐标系中,∠ACB=90°,AC=BC,点B,C的坐标分别为(-2,-4),(-4,0).
(1)求点A的坐标及直线AB的表达式;
(2)若P是x轴上一点,且S△ABP=6,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】为开展全科大阅读活动,学校花费了3400元在书店购买了40套古典文学书籍和20套现代文学书籍,每套现代文学书籍比每套古典文学书籍多花20元.
(1)求每套古典文学习书籍和现代文学书籍分别是多少元?
(2)为满足学生的阅读需求,学校计划用不超过2500元再次购买古典文学和现代文学书籍共40套,经市场调查得知,每套古典文学书籍价格上浮了20%,每套现代文学书籍价格下调了10%,学校最多能购买多少套现代文学书籍?
查看答案和解析>>
科目: 来源: 题型:
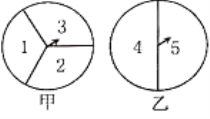
【题目】如图,甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形.小夏和小秋利用它们来做决定获胜与否的游戏.规定小夏转甲盘一次、小秋转乙盘一次为一次游戏(当指针指在边界线上时视为无效,重转).
(1)小夏说:“如果两个指针所指区域内的数之和为6或7,则我获胜;否则你获胜”.按小夏设计的规则,请你写出两人获胜的可能性分别是多少?
(2)请你对小夏和小秋玩的这种游戏设计一种公平的游戏规则,并用一种合适的方法(例如:树状图,列表)说明其公平性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com