
科目: 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点
中的点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() (其中
(其中![]() 为常数,且
为常数,且![]() ),则称点
),则称点![]() 为点
为点![]() 的“
的“![]() 属派生点”.例如:
属派生点”.例如:![]() 的“2属派生点”为
的“2属派生点”为![]() ,即
,即![]() .
.
(l)求点![]() 的“3属派生点”
的“3属派生点”![]() 的坐标:
的坐标:
(2)若点![]() 的“5属派生点”
的“5属派生点”![]() 的坐标为
的坐标为![]() ,求点
,求点![]() 的坐标:
的坐标:
(3)若点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 的“收属派生点”为
的“收属派生点”为![]() 点,且线段
点,且线段![]()
![]() 的长度为线段
的长度为线段![]() 长度的2倍,求k的值.
长度的2倍,求k的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】(阅读材料)
南京市地铁公司规定:自2019年3月31日起,普通成人持储值卡乘坐地铁出行,每个自然月内,达到规定消费累计金额后的乘次,享受相应的折扣优惠(见图).地铁出行消费累计金额月底清零,次月重新累计.

比如:李老师二月份无储值卡消费260元,若采用新规持储值卡消费,则需付费150×0.95+50×0.9+60×0.8=235.5元.
(解决问题)
甲、乙两个成人二月份无储值卡乘坐地铁消费金额合计300元(甲消费金额超过150元,但不超过200元).若两人采用新规持储值卡消费,则共需付费283.5元.求甲、乙二月份乘坐地铁的消费金额各是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】某区对2019年参加学业水平考试的3000名初中毕业生进行了一次视力抽样调查,绘制出如下频数分布表和频数分布直方图.某区2019年初中毕业生视力抽样频数分布表
视力
| 频数/人 50 50 | 频率 0.25 0.15 |
| 60 | 0.30 |
|
| 0.25 |
| 10 |
|
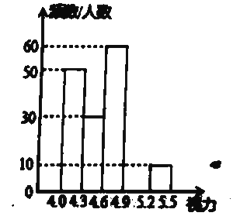
请根据图表信息回答下列问题:
(1)在频数分布表中,求![]() 的值和
的值和![]() 的值:
的值:
(2)将频数分布直方图补充完整;
(3)若视力在4.9以上(含4.9)均为正常,根据以上信息估计全区初中毕业生中
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
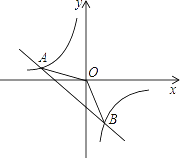
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△AOB的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知OP平分∠AOB,∠DCE的顶点C在射线OP上,射线CD交射线OA于点F,射线CE交射线OB于点G.
(1)如图1,若CD⊥OA,CE⊥OB,请直接写出线段CF与CG的数量关系;
(2)如图2,若∠AOB=120,∠DCE=∠AOC,试判断线段CF与CG的数量关系,并说明理由.
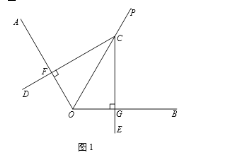
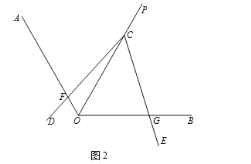
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )

A.AQ= PQ B.AQ=3PQ C.AQ=![]() PQ D.AQ=4PQ
PQ D.AQ=4PQ
查看答案和解析>>
科目: 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(2,1),B(﹣1,1),C(﹣1,﹣3),D(2,﹣3),点P从点A出发,以每秒1个单位长度的速度沿A﹣B﹣C﹣D﹣A…的规律在图边形ABCD的边上循环运动,则第2019秒时点P的坐标为( )

A. (1,1)B. (0,1)C. (﹣1,1)D. (2,﹣1)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在等边△ABC中,点D,E分别在边AC,AB上,且AD=BE,BD,CE交于点P,CF⊥BD,垂足为点F.
(1)求证:BD=CE;
(2)若PF=3,求CP的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.

(1)求A,B,C三点的坐标;
(2)若点P为线段BC上一点(不与B,C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求点P的坐标;
(3)在(2)的条件下,当△BCM的面积最大时,在抛物线的对称轴上存在一点Q,使得△CNQ为直角三角形,求点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com