【题目】已知等边三角形的高为6，在这个三角形所在的平面内有一个点，若点到的距离是1，点到的距离是2，则点到的最小距离与最大距离分别是_______.

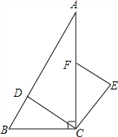
（1）求证：△BCD≌△FCE；

（2）若EF∥CD，求∠BDC的度数．

（1）在图中画出△ABC关于y轴对称的图形△A1B1C1；（其中A1、B1、C1分别是A、B、C的对应点，不写画法．）

（2）写出点A1、B1、C1的坐标；

（3）求出△A1B1C1的面积．

【题目】已知一次函数和反比例函数．

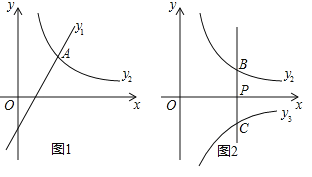
如图1，若，且函数、的图象都经过点．求m，k的值；

如图2，过点作y轴的平行线l与函数的图象相交于点B，与反比例函数的图象相交于点C．

若，直线l与函数的图象相交点当点B、C、D中的一点到另外两点的距离相等时，求的值；

过点B作x轴的平行线与函数的图象相交与点当的值取不大于1的任意实数时，点B、C间的距离与点B、E间的距离之和d始终是一个定值．求此时k的值及定值d．

【题目】【探究函数y＝x＋的图象与性质】

(1)函数y＝x＋的自变量x的取值范围是________；

(2)下列四个函数图象中，函数y＝x＋的图象大致是________；

(3)对于函数y＝x＋，求当x＞0时，y的取值范围．请将下列的求解过程补充完整．

解：∵x＞0，∴y＝x＋＝()2＋＝＋________．

∵≥0，∴y≥________．

【拓展运用】

(4)若函数y＝，求y的取值范围．

【题目】为应对越来越复杂的交通状况，某城市对其道路进行拓宽改造，工程队在工作了一段时间后，因雨被迫停工几天，随后工程队加快了施工进度，按时完成了拓宽改造任务.下面能反映该工程尚未改造的道路（米）与时间（天）的关系的大致图象是（ ）

A.B.C.D.

（1）这场沙尘暴的最高风速是多少？最高风速维持了多长时间；

（2）求出当x≥20时，风速y（千米/小时）与时间x（小时）之间的函数关系？

（3）在这次沙尘暴的形成过程中，当风速不超过10千米/小时称为“安全时刻”，其余时刻是“危险时刻”．问这次风暴的整个过程中，“危险时刻”一共有多长时间？

小明在数学课外小组活动时遇到这样一个问题：

如果一个不等式中含有绝对值，并且绝对值符号中含有未知数，我们把这个不等式叫做绝对值不等式，求绝对值不等式|x|＞3的解集．

小明同学的思路如下：

先根据绝对值的定义，求出|x|恰好是3时x的值，并在数轴上表示为点A，B，如图所示．观察数轴发现，以点A，B为分界点把数轴分为三部分：

点A左边的点表示的数的绝对值大于3；

点A，B之间的点表示的数的绝对值小于3；

点B右边的点表示的数的绝对值大于3．

因此，小明得出结论绝对值不等式|x|＞3的解集为：x＜-3或x＞3．

参照小明的思路，解决下列问题：

（1）请你直接写出下列绝对值不等式的解集．

①|x|＞1的解集是 ．

②|x|＜2.5的解集是 ．

（2）求绝对值不等式2|x-3|+5＞13的解集．

（3）直接写出不等式x2＞4的解集是 .

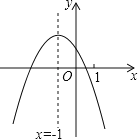
A. 4个 B. 3个 C. 2个 D. 1个