
科目: 来源: 题型:
【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ADC=90°,点E是BC边上一动点,联结AE,过点E作AE的垂线交直线CD于点F.已知AD=4cm,CD=2cm,BC=5cm,设BE的长为x cm,CF的长为y cm.

小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行探究.下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:

(说明:补全表格时相关数据保留一位小数)
(2)建立直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题: 当BE=CF时,BE的长度约为 cm.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了推进书香校园建设,加强学生课外阅读,某校开展了“走近名家名篇”的主题活动;学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分,如下:
时间(单位: | 频数(人数) | 频率 |
| 2 | 0.04 |
| 3 | 0.06 |
| 15 | 0.30 |
|
| 0.50 |
| 5 |
|

请根据图表信息回答下列问题:
(1)频数分布表中的![]() _________,
_________,![]() ___________;
___________;
(2)将频数分布直方图补充完整;
(3)学校将每周课外阅读时间在8小时以上的学生评为“阅读之星”,请你估计该校1200名学生中评为“阅读之星”的有多少人?
查看答案和解析>>
科目: 来源: 题型:
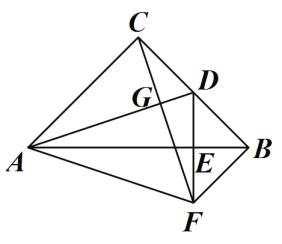
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,D为BC中点,DE⊥AB,垂足为点E,过点B作BF∥AC交DE的延长线于点F,连接CF、AF、AD,AD与CF交于点G.
(1)求证:△ACD≌△CBF;
(2)AD与CF的关系是 ;
(3)求证:△ACF是等腰三角形;
(4)△ACF可能是等边三角形吗? (填“可能”或“不可能”).
查看答案和解析>>
科目: 来源: 题型:
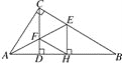
【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,AE平分∠CAB交CD于点F,交BC于点E,EH⊥AB,垂足为H,连接FH.
求证:(1)CF=CE
(2)四边形CFHE是平行四边形.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在四边形ABCD中,BD是一条对角线,∠DBC=30°,∠DBA=45°,∠C=70°.若DC=a,AB=b, 请写出求tan∠ADB的思路.(不用写出计算结果)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点M在BA的延长线上,MD切⊙O于点D,过点B作BN⊥MD于点C,连接AD并延长,交BN于点N.
(1)求证:AB=BN;
(2)若⊙O半径的长为3,cosB=![]() ,求MA的长.
,求MA的长.

查看答案和解析>>
科目: 来源: 题型:
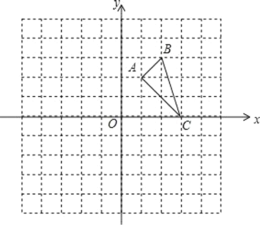
【题目】在平面直角坐标系中,△ABC的位置如图所示,三个顶点的坐标分别为:A(1,2)、B(2,3)、C(3,0).
(1)现将△ABC先向左平移5个单位长度,再向上平移2个单位长度,得到△A1B1C1,请在平面直角坐标系中画出△A1B1C1.
(2)此时平移的距离是 ;
(3)在平面直角坐标系中画出△ABC关于点O成中心对称的△A2B2C2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com