
科目: 来源: 题型:
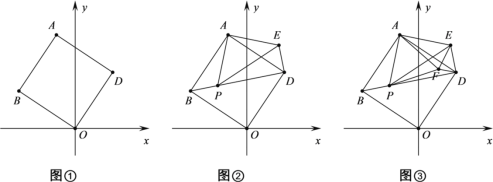
【题目】如图①,将正方形ABOD放在平面直角坐标系中,O是坐标原点,点D的坐标为(2,3),
(1)点B的坐标为 ;
(2)若点P为对角线BD上的动点,作等腰直角三角形APE,使∠PAE=90°,如图②,连接DE,则BP与DE的关系(位置与数量关系)是 ,并说明理由;
(3)在(2)的条件下,再作等边三角形APF,连接EF、FD,如图③,在 P点运动过程中当EF取最小值时,此时∠DFE= °;
(4)在(1)的条件下,点 M在 x 轴上,在平面内是否存在点N,使以 B、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线![]() 交
交![]() 轴于点
轴于点![]() 、点
、点![]() ,交
,交![]() 轴于点C,且S△ABC=6.
轴于点C,且S△ABC=6.
(1)求![]() 两点的坐标;
两点的坐标;
(2)求△ABC的外接圆与抛物线的对称轴的交点坐标;
(3)点E为抛物线上的一动点(点![]() 异于
异于![]() ,且
,且![]() 在对称轴右侧),直线
在对称轴右侧),直线![]() 交对称轴于N,
交对称轴于N,
直线BE交对称轴于![]() ,对称轴交
,对称轴交![]() 轴于
轴于![]() ,试确定
,试确定![]() 、
、![]() 的数量关系并说明理由.
的数量关系并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知△ABC中, ![]() ,
, ![]() ,△CDE中,
,△CDE中, ![]() ,CD=DE=5,
,CD=DE=5,
连接接BE,取BE中点F,连接AF、DF.
(1)如图1,若![]() 三点共线,
三点共线, ![]() 为
为![]() 中点.
中点.
①直接指出![]() 与
与![]() 的关系______________;
的关系______________;
②直接指出![]() 的长度______________;
的长度______________;
(2)将图(1)中的△CDE绕![]() 点逆时针旋转
点逆时针旋转![]() (如图2,
(如图2, ![]() ),试确定
),试确定![]() 与
与![]() 的关系,并说明理由;
的关系,并说明理由;
(3)在(2)中,若![]() ,请直接指出点
,请直接指出点![]() 所经历的路径长.
所经历的路径长.


图1 图2
查看答案和解析>>
科目: 来源: 题型:
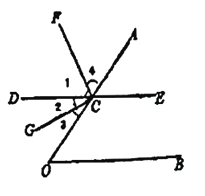
【题目】请在横线上填上合适的内容,完成下面的证明:
如图,射线AH交折线ACGFEN于点B、D、E.已知∠A=∠1,∠C=∠F,BM平分∠CBD,EN平分∠FEH.求证:∠2=∠3.

证明:∵∠A=∠1(已知)
∴AC∥GF( )
∴( )( )
∵∠C=∠F(已知)
∴∠F=∠G
∴( )( )
∴( )( )
∵BM平分∠CBD,EN平分∠FEH
∴∠2= ∠3=
∴∠2=∠3
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.

查看答案和解析>>
科目: 来源: 题型:
【题目】定义:在平面直角坐标系中,对于任意两点![]() ,
,![]() ,若点
,若点![]() 满足
满足![]() ,
,![]() ,那么称点
,那么称点![]() 是点
是点![]() ,
,![]() 的融合点.
的融合点.
例如:![]() ,
,![]() ,当点
,当点![]() 满是
满是![]() ,
,![]() 时,则点
时,则点![]() 是点
是点![]() ,
,![]() 的融合点,
的融合点,

(1)已知点![]() ,
,![]() ,
,![]() ,请说明其中一个点是另外两个点的融合点.
,请说明其中一个点是另外两个点的融合点.
(2)如图,点![]() ,点
,点![]() 是直线
是直线![]() 上任意一点,点
上任意一点,点![]() 是点
是点![]() ,
,![]() 的融合点.
的融合点.
①试确定![]() 与
与![]() 的关系式.
的关系式.
②若直线![]() 交
交![]() 轴于点
轴于点![]() ,当
,当![]() 为直角三角形时,求点
为直角三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,在长方形![]() 中,
中,![]() 。点
。点![]() 从
从![]() 出发,沿
出发,沿![]() 路线运动,到
路线运动,到![]() 停止;点
停止;点![]() 出发时的速度为每秒
出发时的速度为每秒![]() ,7秒时点
,7秒时点![]() 的速度变为每秒
的速度变为每秒![]() ,图②是点
,图②是点![]() 出发
出发![]() 秒后,
秒后,![]() 的面积
的面积![]() 与
与![]() (秒)的关系图象;
(秒)的关系图象;

(1)根据题目提供的信息,求出![]() 的值为______________、
的值为______________、![]() 的值为_________
的值为_________![]() 的值为___________;
的值为___________;
(2)设点![]() 离开点
离开点![]() 的路程为
的路程为![]() ,
,
①7.5秒时,![]() 的值为_____________________;
的值为_____________________;
②请求出当动点![]() 改变速度后,
改变速度后,![]() 与
与![]() 的关系式;
的关系式;
(3)点![]() 出发后几秒,
出发后几秒,![]() 的面积
的面积![]() 是长方形
是长方形![]() 面积的
面积的![]() ?并说明理由。
?并说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】下表数据是科研小组在某地区根据调查获取的:“距离地面的高度(千米)与此处的温度(摄氏度)”的关系。
距离地面高度/千米 | 0 | 1 | 2 | 3 | 4 | 5 |
温度/摄氏度 | 20 | 14 | 8 | 2 | -4 | -10 |
根据上表,请你回答:
(1)上表中___________是自变量;_________________是因变量;
(2)如果用![]() 表示距离地面的高度(千米),
表示距离地面的高度(千米),![]() 表示温度(摄氏度),请你写出
表示温度(摄氏度),请你写出![]() 与
与![]() 的关系式____________________________________;
的关系式____________________________________;
(3)请你利用(2)的结论,求该地区:①距离地面6.2千米的高空温度是多少?②当高空某处温度为-52度时,该处的高度是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】推理填空:如图,点![]() 在
在![]() 的一边
的一边![]() 上,过点
上,过点![]() 的直线
的直线![]() 平行直线
平行直线![]() ,
,![]() 平分
平分![]() ,
,![]() 于点
于点![]() .
.
(1)求证:![]() 平分
平分![]() ;
;
(2)当![]() 为多少度时,
为多少度时,![]() 平分
平分![]() ,并说明理由。
,并说明理由。
(1)证明:∵![]() (已知)
(已知)
∴![]() (垂直定义)
(垂直定义)
即![]()
又∵![]() (平角定义)
(平角定义)
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() (角平分线定义)
(角平分线定义)
∴![]() (_____________________)
(_____________________)
即![]() 平分
平分![]() ;
;
(2)解:![]() 时,
时,![]() 平分
平分![]() ,理由如下:
,理由如下:
∵![]() ,
,
∴![]() (____________________________),
(____________________________),
∴![]() _________________°
_________________°
又∵![]() 平分
平分![]() ,
,
∴![]() °,
°,
∴![]() (等量代换)
(等量代换)
即![]() 平分
平分![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com