
科目: 来源: 题型:
【题目】【概念学习】规定:求若干个相同的有理数(均不等于0)的除法运算叫除方,如![]() ,
, ![]() 等.类比有理数乘方,我们把
等.类比有理数乘方,我们把![]() 记作
记作![]() ,读作“2的圈3次方”,
,读作“2的圈3次方”, ![]() 记作
记作![]() ,读作“
,读作“![]() 的圈4次方”.一般地,把
的圈4次方”.一般地,把![]() (
(![]() ≠0)记作
≠0)记作![]() ,读作“a的圈c次方”.
,读作“a的圈c次方”.
【初步探究】
(1)直接写出计算结果: ![]() =______________,
=______________, ![]() =______________.
=______________.
(2)关于除方,下列说法错误的是( )
A.任何非零数的圈3次方都等于它的倒数 B.对于任何正整数c, ![]() =1
=1
C. ![]() D.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数
D.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数
【深入思考】
我们知道有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
![]()
![]() =
=![]() =
=![]()
![]()
(1)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式.
![]() =___________;
=___________; ![]() =_____________;
=_____________; ![]() =____________.
=____________.
(2)想一想:将一个非零有理数a的圈c(c≥3)次方写成幂的形式等于___________.
(3)算一算: ![]()
/span>
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两名采购员同去一家饲料公司购买两次饲料.两次饲料的价格分别为![]() 元/千克和
元/千克和![]() 元/千克(
元/千克(![]() 、
、![]() 都为正数,且
都为正数,且![]() ),两名采购员的购货方式不同,其中甲每次购买800千克;乙每次用去800元,而不管购买多少饲料.
),两名采购员的购货方式不同,其中甲每次购买800千克;乙每次用去800元,而不管购买多少饲料.
(1)用含![]() 、
、![]() 的代数式表示甲、乙两名采购员两次购买饲料的平均单价各是多少?
的代数式表示甲、乙两名采购员两次购买饲料的平均单价各是多少?
(2)若规定:谁两次购买饲料的平均单价低,谁的购货方式合算,请你判断甲、乙两名采购员购货方式哪个更合算?说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:∠ACB=90°,AC=BC,AD⊥CM,BE⊥CM,垂足分别为D,E,

(1)如图1,
①线段CD和BE的数量关系是 ;
②请写出线段AD,BE,DE之间的数量关系并证明.
(2)如图2,上述结论②还成立吗?如果不成立,请直接写出线段AD,BE,DE之间的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1, ![]() ABCD和
ABCD和![]() AEFG是两个能完全重合的平行四边形,现从AB与AE重合时开始,将
AEFG是两个能完全重合的平行四边形,现从AB与AE重合时开始,将![]() ABCD固定不动,
ABCD固定不动, ![]() AEFG绕点A逆时针旋转,旋转角为α(0°<α<360°),AB=a,BC=2a;并发现:如图2,当
AEFG绕点A逆时针旋转,旋转角为α(0°<α<360°),AB=a,BC=2a;并发现:如图2,当![]() AEFG旋转到点E落在AD上时,FE的延长线恰好通过点C.
AEFG旋转到点E落在AD上时,FE的延长线恰好通过点C.
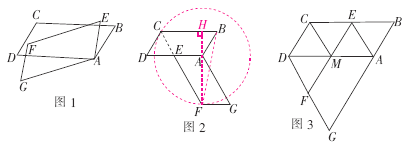
探究一:
(1)在图2的情形下,求旋转角α的度数;
探究二:
(2)如图3,当![]() AEFG旋转到点E落在BC上时,EF与AD相交于点M,连接CM,DF,请你判断四边形CDFM的形状,并给予证明;
AEFG旋转到点E落在BC上时,EF与AD相交于点M,连接CM,DF,请你判断四边形CDFM的形状,并给予证明;
探究三:
(3)如图1,连接CF,BF,在旋转过程中△BCF的面积是否存在最大的情形,如果存在,求出最大面积,如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明解方程![]() =3出现了错误,解答过程如下:
=3出现了错误,解答过程如下:
方程两边都乘以(x-2),得1-(1-x)=3(第一步)
去括号,得1-1+x=3(第二步)
移项,合并同类项,得x=3(第三步)
检验,当x=3时x-2≠0(第四步)
所以x=3是原方程的解.(第五步)
(1)小明解答过程是从第____步开始出错的,原方程化为第一步的根据是_____.
(2)请写出此题正确的解答过程.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌![]() ,△AEB≌
,△AEB≌![]() ,且
,且![]() ,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )
,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )

A.105°B.100°C.110°D.115°
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=-x2+bx+c的顶点P的坐标为(n,n2+2n+1)(n≥1).
(1)求b与n,c与n之间的关系式;
(2)若抛物线y=-x2+bx+c与x轴交于点A,B(点A在点B的左边),点P到AB的距离等于线段AB长的2倍,求此抛物线y=-x2+bx+c的解析式;
(3)设抛物线y=-x2+bx+c与y轴交于点D,O为原点,矩形OEFD的顶点E,F分别在x轴和该抛物线上,当矩形OEFD的面积为20时,求点P的坐标.
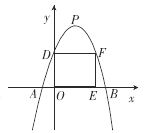
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线l1的表达式为:y=-3x+3,且直线l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积;
(4)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,求点P的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】某检修小组乘汽车从![]() 地出发,在东西走向的马路上检修线路,如果规定向东行驶为正,一天中七个检修点的行驶记录如下(单位:
地出发,在东西走向的马路上检修线路,如果规定向东行驶为正,一天中七个检修点的行驶记录如下(单位:![]() ):
):
-4,+7,-9,+8,+6,-4,-3.
(1)收工时汽车共行驶了多少千米?
(2)收工时,汽车距![]() 地多远?
地多远?
(3)在检修时,第几个检修点离![]() 地最远,最远距离是多少?
地最远,最远距离是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】某市自来水公司为限制单位用水,每月只给某单位计划内用水 3000 吨,计划内用水每吨收费 0.5元,超计划部分每吨按 0.8 元收费.
(1)写出该单位水费 y(元)与每月用水量 x(吨)之间的函数关系式:(写出自变量取值范围)
①用水量小于等于 3000 吨 ;
②用水量大于 3000 吨 .
(2)某月该单位用水 3200 吨,水费是 元;若用水 2800 吨,水费 元.
(3)若某月该单位缴纳水费 1580 元,则该单位用水多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com