
科目: 来源: 题型:
【题目】已知AB∥CD,在AB,CD内有一条折线EGF.
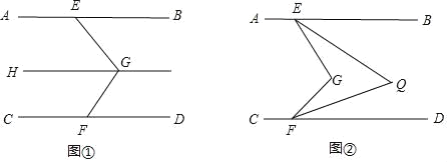
(1)如图①,过点G作GH∥AB,求证:∠BEG+∠DFG=∠EGF;
(2)如图②,已知∠BEG的平分线与∠DFG的平分线相交于点Q,请探究∠EGF与∠EQF的数量关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】李明准备进行如下操作实验,把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的说法正确吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校的数学小组将七年级学生某个星期天阅读时间t(单位:分钟)的调查数据进行整理,绘制出如下不完整的频数分布表和频数分布直方图;

阅读时间分钟 | 频数(人数) | 频率 |
30≤t<40 | 10 | 5% |
40≤t<50 | 40 | m |
50≤t<60 | a | 40% |
60≤t<70 | b | n |
70≤t<80 | 20 | 10% |
(1)求a=________,b=________,m=________,n=________;
(2)补全频数分布直方图;
(3)如果阅读时间不少于60分钟即为达标,则达标人数共有多少人?若七年级学生在某时间段内阅读的人数有500人,估计约有多少人达标?
查看答案和解析>>
科目: 来源: 题型:
【题目】某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人.投票结果统计如图一:

其次,对三名候选人进行了笔试和面试两项测试.各项成绩如右表所示:图二是某同学根据上表绘制的一个不完整的条形图.请你根据以上信息解答下列问题:
(1)补全图一和图二.
(2)请计算每名候选人的得票数.
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2:5:3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 92 | 90 | 95 |
面试 | 85 | 95 | 80 |
查看答案和解析>>
科目: 来源: 题型:
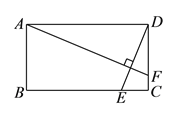
【题目】如图,矩形![]() 中,
中, ![]() ,
, ![]() ,动点
,动点![]() 在边
在边![]() 上,连结
上,连结![]() ,过点
,过点![]() 作
作![]() 的垂线
的垂线![]() ,交直线
,交直线![]() 于点
于点![]() .设
.设![]() ,
, ![]() .
.
(![]() )求
)求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(![]() )当
)当![]() 时,求
时,求![]() 的长.
的长.
(![]() )若直线
)若直线![]() 与线段
与线段![]() 延长线交于点
延长线交于点![]() ,当
,当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OD平分∠BOF,OE⊥CD于O,若∠EOF=α,下列说法①∠AOC=α﹣90°;②∠EOB=180°﹣α;③∠AOF=360°﹣2α,其中正确的是( )
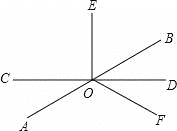
A. ①②B. ①③C. ②③D. ①②③
查看答案和解析>>
科目: 来源: 题型:
【题目】数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题.下面我们来探究“由数思形,以形助数”的方法在解决代数问题中的应用.
探究一:求不等式|x﹣1|<2的解集
(1)探究|x﹣1|的几何意义
如图①,在以O为原点的数轴上,设点A′对应的数是x﹣1,有绝对值的定义可知,点A′与点O的距离为
|x﹣1|,可记为A′O=|x﹣1|.将线段A′O向右平移1个单位得到线段AB,此时点A对应的数是x,点B对应的数是1.因为AB=A′O,所以AB=|x﹣1|,因此,|x﹣1|的几何意义可以理解为数轴上x所对应的点A与1所对应的点B之间的距离AB.

(2)求方程|x﹣1|=2的解
因为数轴上3和﹣1所对应的点与1所对应的点之间的距离都为2,所以方程的解为3,﹣1.
(3)求不等式|x﹣1|<2的解集
因为|x﹣1|表示数轴上x所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点对应的数x的范围.请写出这个解集:_________________________________.
探究二:探究![]() 的几何意义
的几何意义
(1)探究![]() 的几何意义
的几何意义
如图③,在直角坐标系中,设点M的坐标为(x,y),过M作MP⊥x轴于P,作MQ⊥y轴于Q,则P点坐标为(x,0),Q点坐标为(0,y),OP=|x|,OQ=|y|,在Rt△OPM中,PM=OQ=|y|,则![]() ,因此,
,因此,![]() 的几何意义可以理解为点M(x,y)与点O(0,0)之间的距离MO.
的几何意义可以理解为点M(x,y)与点O(0,0)之间的距离MO.

(2)探究![]() 的几何意义
的几何意义
如图④,在直角坐标系中,设点A′的坐标为(x﹣1,y﹣5),由探究二(1)可知,![]() ,将线段A′O先向右平移1个单位,再向上平移5个单位,得到线段AB,此时点A的坐标为(x,y),点B的坐标为(1,5),因为AB=A′O,所以
,将线段A′O先向右平移1个单位,再向上平移5个单位,得到线段AB,此时点A的坐标为(x,y),点B的坐标为(1,5),因为AB=A′O,所以![]() ,因此
,因此![]() 的几何意义可以理解为点A(x,y)与点B(1,5)之间的距离AB.
的几何意义可以理解为点A(x,y)与点B(1,5)之间的距离AB.

(3)探究![]() 的几何意义,根据探究二(2)所得的结论,请写出
的几何意义,根据探究二(2)所得的结论,请写出![]() 的几何意义可以理解为:________________.
的几何意义可以理解为:________________.
(4)![]() 的几何意义可以理解为:________________________________.
的几何意义可以理解为:________________________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵10元,用350元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)计划购买这两种商品共50件,且投入的经费不超过3200元,那么最多购买多少件甲种商品?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点B、C分别在函数![]() 的图像上,AB∥x轴,AC∥y轴,已知点A的坐标为(2,m)(
的图像上,AB∥x轴,AC∥y轴,已知点A的坐标为(2,m)(![]() ),延长OA交反比例函数
),延长OA交反比例函数![]() 的图像交于点P,
的图像交于点P,
(1)当点P横坐标为3,求m的值;
(2)连接CO,当AC=OA时,求m的值;
(3)连接BP、CP,![]() 的值是否随m的变化而变化?若变化,说明理由;若不变,求出
的值是否随m的变化而变化?若变化,说明理由;若不变,求出![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com