
科目: 来源: 题型:
【题目】某检修小组乘一辆检修车沿铁路检修,规定向东走为正,向西走为负,该小组的出发地记为A,某天检修完毕时,行走记录(单位.千米)如下.
+10,-2,+3,-1,+5,-3,-2,+11,+3,-4,+6.
(1)问收工时,检修小组距出发地有多远?在东侧还是西侧?
(2)距离A最近的一次是哪一次?距离多远?
(3)若检修车每千米耗油2.8升,求从出发到收工共耗油多少升?
查看答案和解析>>
科目: 来源: 题型:
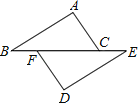
【题目】如图,点B,F,C,E在一条直线上BF=CE,AC=DF.
(1)在下列条件 ①∠B=∠E;②∠ACB=∠DFE;③AB=DE;④AC∥DF中,只添加一个条件就可以证得△ABC≌△DEF,则所有正确条件的序号是 .
(2)根据已知及(1)中添加的一个条件证明∠A=∠D.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,平面直角坐标系xOy中,点A在第一象限,B(2,0),∠AOB=60°,∠ABO=90°.在x轴上取一点P(m,0),过点P作直线l垂直于直线OA,将OB关于直线l的对称图形记为O′B′,当O′B′和过A点且平行于x轴的直线有交点时,m的取值范围为( )

A.m≥4B.m≤6C.4<m<6D.4≤m≤6
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=12,BC=9,AB=15,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3个单位,设运动的时间为t秒.
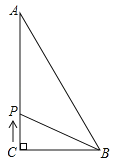
(1)当t= 时,CP把△ABC的面积分成相等的两部分;
(2)当t=5时,CP把△ABC分成的两部分面积之比是![]() = .
= .
(3)若△BPC的面积为18,试求t的值.
查看答案和解析>>
科目: 来源: 题型:
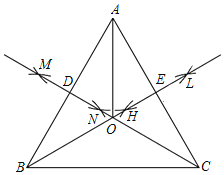
【题目】已知等边三角形ABC.如图,
(1)分别以点A,B为圆心,大于的![]() AB长为半径作弧,两弧相交于M,N两点;
AB长为半径作弧,两弧相交于M,N两点;
(2)作直线MN交AB于点D;
(2)分别以点A,C为圆心,大于![]() AC的长为半径作弧,两弧相交于H,L两点;
AC的长为半径作弧,两弧相交于H,L两点;
(3)作直线HL交AC于点E;
(4)直线MN与直线HL相交于点O;
(5)连接OA,OB,OC.
根据以上作图过程及所作图形,下列结论:①OB=2OE;②AB=2OA;③OA=OB=OC;④∠DOE=120°,正确的是( )
A.①②③④B.①③④C.①②③D.③④
查看答案和解析>>
科目: 来源: 题型:
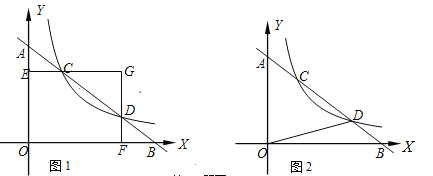
【题目】探究:如图1 ,直线l与坐标轴的正半轴分别交于A,B两点,与反比例函数![]() 的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(a,b).
的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(a,b).
(1)若![]() ,请用含n的代数式表示
,请用含n的代数式表示![]() ;
;
(2)求证: ![]() ;
;
应用:如图2,直线l与坐标轴的正半轴分别交于点A,B两点,与反比例函数![]() 的图象交于点C,D两点(点C在点D的左边),已知
的图象交于点C,D两点(点C在点D的左边),已知![]() ,△OBD的面积为1,试用含m的代数式表示k.
,△OBD的面积为1,试用含m的代数式表示k.
查看答案和解析>>
科目: 来源: 题型:
【题目】江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.
查看答案和解析>>
科目: 来源: 题型:
【题目】给出下列四个关于是否成反比例的命题,判断它们的真假.
(1)面积一定的等腰三角形的底边长和底边上的高成反比例;
(2)面积一定的菱形的两条对角线长成反比例;
(3)面积一定的矩形的两条对角线长成反比例;
(4)面积一定的直角三角形的两直角边长成比例.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)阅读理解:
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com