
科目: 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=α,点P是△ABC内一点,且![]() .连接PB,试探究PA,PB,PC满足的等量关系.
.连接PB,试探究PA,PB,PC满足的等量关系.
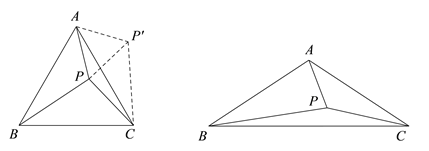
图1 图2
(1)当α=60°时,将△ABP绕点A逆时针旋转60°得到![]() ,连接
,连接![]() ,如图1所示.
,如图1所示.
由![]() ≌
≌![]() 可以证得
可以证得![]() 是等边三角形,再由
是等边三角形,再由![]() 可得∠APC的大小为 度,进而得到
可得∠APC的大小为 度,进而得到![]() 是直角三角形,这样可以得到PA,PB,PC满足的等量关系为 ;
是直角三角形,这样可以得到PA,PB,PC满足的等量关系为 ;
(2)如图2,当α=120°时,请参考(1)中的方法,探究PA,PB,PC满足的等量关系,并给出证明;
(3)PA,PB,PC满足的等量关系为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,是一个“有理数转换器”(箭头是数进入转换器的路径,方框是对进入的数进行转换的转换器)
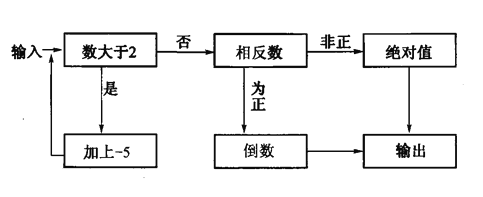
(1)当小明输入-3、![]() 、0.4这三个数时,三次输出的结果分别是 、_______、 .
、0.4这三个数时,三次输出的结果分别是 、_______、 .
(2)你认为当输入 时(写出2个即可),其输出结果是0?
(3)你认为这个“有理数转换器”不可能输出 数?
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 的顶点为A.
的顶点为A.
(1)求点A的坐标;

(2)将线段![]() 沿
沿![]() 轴向右平移2个单位得到线段
轴向右平移2个单位得到线段![]() .
.
①直接写出点![]() 和
和![]() 的坐标;
的坐标;
②若抛物线![]() 与四边形
与四边形![]() 有且只有两个公共点,结合函数的图象,求
有且只有两个公共点,结合函数的图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的性质.
的性质.
(1)先从简单情况开始探究:
① 当函数为![]() 时,
时, ![]() 随
随![]() 增大而 (填“增大”或“减小”);
增大而 (填“增大”或“减小”);
② 当函数为![]() 时,它的图象与直线
时,它的图象与直线![]() 的交点坐标为 ;
的交点坐标为 ;
(2)当函数为![]() 时,
时,
下表为其y与x的几组对应值.
x | … |
| 0 | 1 |
| 2 |
| 3 | 4 |
| … |
y | … |
|
| 1 |
| 2 |
| 3 | 7 |
| … |

①如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象;
②根据画出的函数图象,写出该函数的一条性质: .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,AM是△ACD的外角∠DAF的平分线.

(1)求证:AM是⊙O的切线;
(2)若∠D = 60°,AD = 2,射线CO与AM交于N点,请写出求ON长的思路.
查看答案和解析>>
科目: 来源: 题型:
【题目】在矩形ABCD中,AB=3,BC=6,P为BC边上一点,△APD为等腰三角形.
(1)小明画出了一个满足条件的△APD,其中PA=PD,如图1所示,则tan ![]() 的值为 ;
的值为 ;
(2)请你在图2中再画出一个满足条件的△APD(与小明的不同),并求此时tan ![]() 的值.
的值.
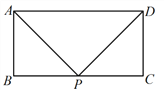

图1 图2
查看答案和解析>>
科目: 来源: 题型:
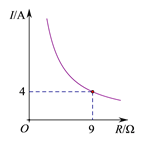
【题目】已知蓄电池的电压U为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.
(1)求这个反比例函数的表达式;
(2)如果以此蓄电池为电源的用电器的限制电流不能超过10A,那么用电器的可变电阻R应控制在什么范围?请根据图象,直接写出结果 .
查看答案和解析>>
科目: 来源: 题型:
【题目】生活与数学
日 | 一 | 二 | 三 | 四 | 五 | 六 |
1 | 2 | 3 | 4 | 5 | 6 | |
7 | 8 | 9 | 10 | 11 | 12 | 13 |
14 | 15 | 16 | 17 | 18 | 19 | 20 |
21 | 22 | 23 | 24 | 25 | 26 | 27 |
(1)姆同学在某月的日历上圈出2×2个数,正方形的方框内的四个数的和是48,那么这四个数是_______.
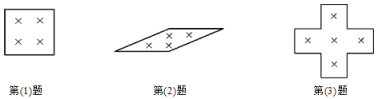
(2)丽也在上面的日历上圈出2×2个数,斜框内的四个数的和是46,则它们分别是_____.
(3)莉也在日历上圈出5个数,呈十字框形,它们的和是55,则中间的数是______.
(4)某月有5个星期日的和是75,则这个月中最后一个星期日是______号?
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是“用三角板画圆的切线”的画图过程.
如图1,已知圆上一点A,画过A点的圆的切线.
![]()

画法:(1)如图2,将三角板的直角顶点放在圆上任一点C(与点A不重合)处,使其一直角边经过点A,另一条直角边与圆交于B点,连接AB;
(2)如图3,将三角板的直角顶点与点A重合,使一条直角边经过点B,画出另一条直角边所在的直线AD.
所以直线AD就是过点A的圆的切线.
请回答:该画图的依据是_______________________________________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读第①小题的计算方法,再计算第②小题.
①–5![]() +(–9
+(–9![]() )+17
)+17![]() +(–3
+(–3![]() )
)
解:原式=[(–5)+(–![]() )]+[(–9)+(–
)]+[(–9)+(–![]() )]+(17+
)]+(17+![]() )+[(–3+(–
)+[(–3+(–![]() )]
)]
=[(–5)+(–9)+(–3)+17]+[(–![]() )+(–
)+(–![]() )+(–
)+(–![]() )+
)+![]() ]
]
=0+(–1![]() )
)
=–1![]() .
.
上述这种方法叫做拆项法.灵活运用加法的交换律、结合律可使运算简便.
②仿照上面的方法计算:(﹣2000![]() )+(﹣1999
)+(﹣1999![]() )+4000
)+4000![]() +(﹣1
+(﹣1![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com