
科目: 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中, ![]() ∥
∥![]() ,∠
,∠![]() =90°,
=90°,![]() =28cm,
=28cm, ![]() =24cm,
=24cm, ![]() =4cm,点
=4cm,点![]() 从点
从点![]() 出发,以1cm/s的速度向点
出发,以1cm/s的速度向点![]() 运动,点
运动,点![]() 从点
从点![]() 同时出发,以2cm/s的速度向点
同时出发,以2cm/s的速度向点![]() 运动,当其中一个动点到达端点停止运动时,另一个动点也随之停止运动。则四边
运动,当其中一个动点到达端点停止运动时,另一个动点也随之停止运动。则四边![]() 的面积
的面积![]() (cm2)与两动点运动的时间
(cm2)与两动点运动的时间![]() (s)的函数图象大致是( )
(s)的函数图象大致是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,顶点为(1,4)的抛物线![]() 与直线
与直线![]() 交于点A(2,2),直线
交于点A(2,2),直线![]() 与
与![]() 轴交于点B与
轴交于点B与![]() 轴交于点C
轴交于点C
(1)求![]() 的值及抛物线的解析式
的值及抛物线的解析式
(2)P为抛物线上的点,点P关于直线AB的对称轴点在![]() 轴上,求点P的坐标
轴上,求点P的坐标
(3)点D为![]() 轴上方抛物线上的一点,点E为轴上一点,以A 、B、E、D为顶点的四边为平行四边形时,直接写出点E的坐标。
轴上方抛物线上的一点,点E为轴上一点,以A 、B、E、D为顶点的四边为平行四边形时,直接写出点E的坐标。
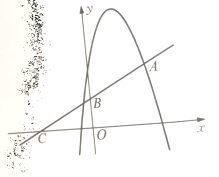
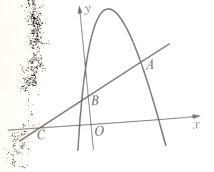
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )

A. 14 B. 16 C. 17 D. 18
查看答案和解析>>
科目: 来源: 题型:
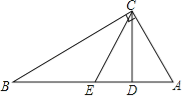
【题目】如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,若点A关于CD所在直线的对称点E恰好为AB的中点,则∠B的度数是( )
A. 60°B. 45°C. 30°D. 75°
查看答案和解析>>
科目: 来源: 题型:
【题目】根据等式和不等式的性质,可以得到:若a-b>0,则a>b;若a-b=0,则a=b;若a-b<0,则a<b.这是利用“作差法”比较两个数或两个代数式值的大小.
(1)试比较代数式5m2-4m+2与4m2-4m-7的值之间的大小关系;
(2)已知A=5m2﹣4(![]() ),B=7(m2﹣m)+3,请你运用前面介绍的方法比较代数式A与B的大小.
),B=7(m2﹣m)+3,请你运用前面介绍的方法比较代数式A与B的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点E,连接OE、AE,过点E作⊙O的切线交边BC于F.

(1)求证:△ODE∽△ECF;
(2)在点O的运动过程中,设DE= ![]() :
:
①求![]() 的最大值,并求此时⊙O的半径长;
的最大值,并求此时⊙O的半径长;
②判断△CEF的周长是否为定值,若是,求出△CEF的周长;否则,请说明理由?
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):

(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?
查看答案和解析>>
科目: 来源: 题型:
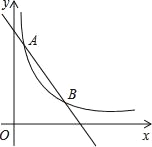
【题目】如图,一次函数y=﹣x+4的图象与反比例函数y=![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
查看答案和解析>>
科目: 来源: 题型:
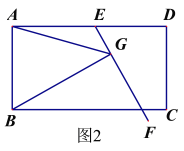
【题目】阅读下列材料:
问题:如图1,在平行四边形ABCD中,E是AD上一点,AE=AB,∠EAB=60°,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
求证:EG =AG+BG.
小明同学的思路是:作∠GAH=∠EAB交GE于点H,构造全等三角形,经过推理解决问题.
参考小明同学的思路,探究并解决下列问题:
(1)完成上面问题中的证明;
(2)如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”,原问题中的其它条件不变(如图2),请探究线段EG、AG、BG之间的数量关系,并证明你的结论.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形ABCD中,E是BC的中点,F是线段CD上的动点.
(1)如图1,若CF=![]() CD,求证:ΔAEF是直角三角形;
CD,求证:ΔAEF是直角三角形;
(2)如图2,若点F与点D重合,点G在ED上,且AG=AD,求证:![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com