
科目: 来源: 题型:
【题目】如图,直线y=![]() x+2分别交x,y轴于点A、C,点P是该直线与反比例函数y=
x+2分别交x,y轴于点A、C,点P是该直线与反比例函数y=![]() 的图象,在第一象限内的交点,PB丄x轴,B为垂足,S△ABP=9.
的图象,在第一象限内的交点,PB丄x轴,B为垂足,S△ABP=9.
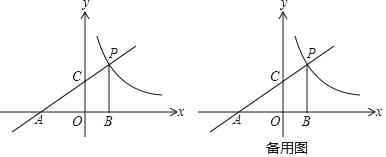
(1)直接写出点A的坐标_____;点C的坐标_____;点P的坐标_____;
(2)已知点Q在反比例函数y=![]() 的图象上,其横坐标为6,在x轴上确定一点M,使MP+MQ最小(保留作图痕迹),并求出点M的坐标;
的图象上,其横坐标为6,在x轴上确定一点M,使MP+MQ最小(保留作图痕迹),并求出点M的坐标;
(3)设点R在反比例函数y=![]() 的图象上,且在直线PB的右侧,做RT⊥x轴,T为垂足,当△BRT与△AOC相似时,求点R的坐标.
的图象上,且在直线PB的右侧,做RT⊥x轴,T为垂足,当△BRT与△AOC相似时,求点R的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)利用求根公式计算,结合①②③你能得出什么猜想?
①方程x2+2x+1=0的根为x1=________,x2=________,x1+x2=________,x1·x2=________.
②方程x2-3x-1=0的根为x1=________,x2=________,x1+x2=________,x1·x2=________.
③方程3x2+4x-7=0的根为x1=_______,x2=________,x1+x2=________,x1·x2=________.
(2)利用求根公式计算:一元二次方程ax2+bx+c=0(a≠0,且b2-4ac≥0)的两根为x1=________,x2=________,x1+x2=________,x1·x2=________.
(3)利用上面的结论解决下面的问题:
设x1、x2是方程2x2+3x-1=0的两个根,根据上面的结论,求下列各式的值:
①![]() ; ②
; ②![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】点A、B在数轴上分别表示有理数a、b, A、B两点之间的距离表示为|AB|,利用数形结合思想回答下列问题:
![]()
(1)数轴上表示﹣3和1两点之间的距离是 ;
(2)数轴上表示x和﹣2的两点之间的距离表示为 ;
(3)若x表示一个有理数,且-3<x<1,则|x﹣1|+|x+3|的最小值是 ;
(4)若x表示一个有理数,且|x﹣1|+|x+3|>4,则有理数x的取值范围是 .
查看答案和解析>>
科目: 来源: 题型:
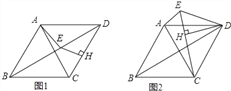
【题目】定义:有一个内角为90°,且对角线相等的四边形称为“不完全矩形”.
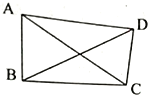
(1)①如图1,在不完全矩形![]() 中,
中,![]() ,若
,若![]() ,
,![]() ,则
,则![]() ____;
____;
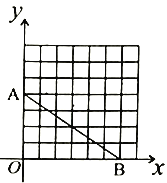
②如图2,在平面直角坐标系中,![]() ,
,![]() ,若整点
,若整点![]() 使得四边形
使得四边形![]() 是不完全矩形,则点
是不完全矩形,则点![]() 的坐标是_____;(整点指横坐标、纵坐标都为整数的点)
的坐标是_____;(整点指横坐标、纵坐标都为整数的点)
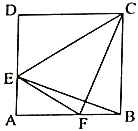
(2)如图3,在正方形![]() 中,点
中,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且
上的点,且![]() ,求证:四边形
,求证:四边形![]() 是不完全矩形.
是不完全矩形.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商店销售甲、乙两种商品,现有如下信息:
请结合以上信息,解答下列问题:
(1)求甲、乙两种商品的进货单价;
(2)已知甲、乙两种商品的零售单价分别为2元、3元,该商店平均每天卖出甲商品500件和乙商品1300件,经市场调查发现,甲种商品零售单价每降0.1元,甲种商品每天可多销售100件,商店决定把甲种商品的零售单价下降m(m>0)元,在不考虑其他因素的条件下,求当m为何值时,商店每天销售甲、乙两种商品获取的总利润为1800元(注:单件利润=零售单价﹣进货单价)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.

(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,在菱形ABCD中,∠ADC=60°,点H为CD上任意一点(不与C、D重合),过点H作CD的垂线,交BD于点E,连接AE.
(1)如图1,线段EH、CH、AE之间的数量关系是 ;
(2)如图2,将△DHE绕点D顺时针旋转,当点E、H、C在一条直线上时,求证:AE+EH=CH.
查看答案和解析>>
科目: 来源: 题型:
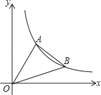
【题目】如图,直线y=![]() x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=
x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=![]() .
.
(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)求S△OAB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com