
科目: 来源: 题型:
【题目】如图,坡AB的坡比为1:2.4,坡长AB=130米,坡AB的高为BT.在坡AB的正面有一栋建筑物CH,点H、A、T在同一条地平线MN上.

(1)试问坡AB的高BT为多少米?
(2)若某人在坡AB的坡脚A处和中点D处,观测到建筑物顶部C处的仰角分别为60°和30°,试求建筑物的高度CH.(精确到米, ![]() ≈1.73,
≈1.73, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目: 来源: 题型:
【题目】用适当的方法解下列方程.
(1)(2x+3)2-16=0;
(2)(x-2)2-3x(x-2)=0.
(3)x2+4x=2
(4)x(x+4)=8x+12
查看答案和解析>>
科目: 来源: 题型:
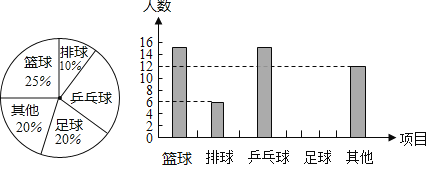
【题目】某课外研究小组为了解学生参加课外体育活动的情况,采取抽样调查的方法从篮球、排球、乒乓球、足球及其他等五个方面调查了若干名同学的兴趣爱好(每人只能选其中一项),并将调查结果绘制成统计图,请根据图中提供的信息解答下列问题:
(1)在这次考察中一共调查了 名学生,请补全条形统计图;
(2)被调查同学中恰好有5名学来自初一12班,其中有2名同学选择了篮球,有3名同学选择了乒乓球,曹老师打算从这5名同学中选择两同学了解他们对体育社团的看法,请用列表法或画树状图法,求选出的两人恰好为一人选择篮球、一人选择乒乓球的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料:
问题:如图1,在平行四边形ABCD中,E是AD上一点,AE=AB,∠EAB=60°,过点E作直线EF,在EF上取一点G.使得∠EGB=∠EAB,连接AG.
求证:EG=AG+BG.
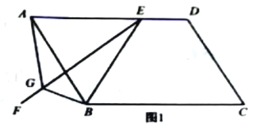
小明同学的思路是:作∠CAM=∠EAB交CE于点H,构造全等三角形,经过推理解决问题.
参考小明同学的思路,探究并解决下列问题:
(1)完成上面问题中的证明;
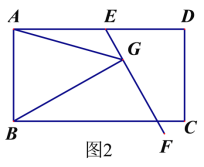
(2)如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”,原问题中的其它条件不变(如图2),请探究线段EC、AG、BG之间的数量关系,并证明你的结论.
解:线段EG、AG、BG之间的数量关系为___________________________________________________.证明:
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,ΔABC中,AB=AC,AB的垂直平分线交AC于P点.
(1)若∠A=35°,则∠BPC=_____;
(2)若AB=5 cm,BC=3 cm,则ΔPBC的周长=_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,有![]() 、
、![]() 、
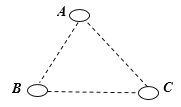
、![]() 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知直角三角形ABC中,∠ACB=90°,E为AB上一点,且CE=EB,ED⊥CB于D,则下列结论中不一定成立的是( )

A.AE=BEB.CE=![]() ABC.∠CEB=2∠AD.AC=
ABC.∠CEB=2∠AD.AC=![]() AB
AB
查看答案和解析>>
科目: 来源: 题型:
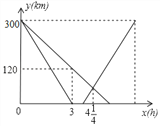
【题目】某客运公司的特快巴士与普通巴士同时从甲地出发,以各自的速度匀速向乙地行驶,普通巴士到达乙地后停止,特快巴士到达乙地停留45分钟后,按原路以另一速度匀速返回甲地,已知两辆巴士分别距乙地的路程y(千米)与行驶时间x(小时)之间的函数图象如图所示.求普通巴士到达乙地时,特快巴士与甲地之间的距离为_____千米.
查看答案和解析>>
科目: 来源: 题型:
【题目】把下列各数按要求分类
+8.3,-4,-0.8,-![]() ,0,π,90,-|-24|,15%,
,0,π,90,-|-24|,15%,![]() 中,
中,
负数有______________________________,
分数有______________________________.
整数有______________________________.
有理数有______________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com