
科目: 来源: 题型:
【题目】在平面直角坐标系中,有两个点![]() ,
,![]() .
.
(1)若![]() 、
、![]() 关于
关于![]() 轴对称,则
轴对称,则![]() _________________,
_________________,![]() ________________.
________________.
(2)若![]() 、
、![]() 关于
关于![]() 轴对称,则
轴对称,则![]() _________________,
_________________,![]() ________________.
________________.
(3)若![]() 、
、![]() 两点重合,将重合后的点绕原点顺时针旋转
两点重合,将重合后的点绕原点顺时针旋转![]() ,此时点的坐标为__________.
,此时点的坐标为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了开展阳光体育运动,某市教体局做了一个随机调查,调查内容是:每天锻炼是否超过1h及锻炼未超过1h的原因.他们随机调查了600名学生,用所得的数据制成了扇形统计图和频数分布直方图(图1、图2).

根据图示,请回答以下问题:
(1)“没时间”的人数是 ,并补全频数分布直方图;
(2)2016年该市中小学生约40万人,按此调查,可以估计2016年全市中小学生每天锻炼超过1h的约有 万人;
(3)在(2)的条件下,如果计划2018年该市中小学生每天锻炼未超过1h的人数降到7.5万人,求2016年至2018年锻炼未超过1h人数的年平均降低的百分率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是用长度相等的小棒按一定规律摆成的一组图案
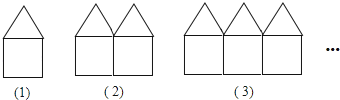
(1)填写下表:
图形序号 | ① | ② | ③ | …… | ⑧ |
每个图案中小棒的数量 | 6 | 11 | …… |
(2)请填写出第![]() 个图案中小棒的数量(用含
个图案中小棒的数量(用含![]() 的代数式表示);
的代数式表示);
(3)第30个图案中小棒有多少根?
查看答案和解析>>
科目: 来源: 题型:
【题目】某校有A、B两个阅览室,甲、乙、丙三名学生各自随机选择其中的一个阅览室阅读.
(1)下列事件中,是必然事件的为( )
A.甲、乙同学都在A阅览室 B.甲、乙、丙同学中至少两人在A阅览室
C.甲、乙同学在同一阅览室 D.甲、乙、丙同学中至少两人在同一阅览室
(2)用画树状图的方法求甲、乙、丙三名学生在同一阅览室阅读的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】平面直角坐标系xOy中,对于点M和图形W,若图形W上存在一点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称点M与图形W是“中心轴对称”的
对于图形![]() 和图形
和图形![]() ,若图形
,若图形![]() 和图形
和图形![]() 分别存在点M和点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称图形
分别存在点M和点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称图形![]() 和图形
和图形![]() 是“中心轴对称”的。
是“中心轴对称”的。
特别地,对于点M和点N,若存在一条经过原点的直线l,使得点M与点N关于直线l对称,则称点M和点N是“中心轴对称”的。
(1)如图1,在正方形ABCD中,点![]() ,点
,点![]() ,
,
①下列四个点![]() ,
,![]() ,
,![]() ,
,![]() 中,与点A是“中心轴对称”的是________;
中,与点A是“中心轴对称”的是________;
②点E在射线OB上,若点E与正方形ABCD是“中心轴对称”的,求点E的横坐标![]() 的取值范围;
的取值范围;
(2)四边形GHJK的四个顶点的坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() ,一次函数
,一次函数![]() 图象与x轴交于点M,与y轴交于点N,若线段与四边形GHJK是“中心轴对称”的,直接写出b的取值范围。
图象与x轴交于点M,与y轴交于点N,若线段与四边形GHJK是“中心轴对称”的,直接写出b的取值范围。

查看答案和解析>>
科目: 来源: 题型:
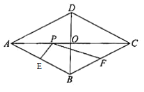
【题目】如图,在菱形ABCD中,对角线AC,相交于点O,![]() cm,
cm,![]() cm,E,F分别是AB,BC的中点,点P是对角线AC上的一个动点,设
cm,E,F分别是AB,BC的中点,点P是对角线AC上的一个动点,设![]() cm,
cm,![]() cm,
cm,![]() cm
cm
小明根据学习函数的经验,分别对这两种函数随自变量的变化而变化的情况进行了探究,下面是小明探究过程,请补充完整:
(1)画函数![]() 的图象
的图象
①按下表自变量的值进行取点、画图、测量,得到了![]() 与x的几组对应值:
与x的几组对应值:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| 1.12 | 0.5 | 0.71 | 1.12 | 1.58 | 2.06 | 2.55 | 3.04 |
②在所给坐标系中描出补全后的表中的各对应值为坐标的点,画出函数![]() 的图象;
的图象;

(2)画函数![]() 的图象
的图象
在同一坐标系中,画出函数![]() 的图象;
的图象;
(3)根据画出的函数![]() 的图象、函数
的图象、函数![]() 的图象,解决问题
的图象,解决问题
①函数![]() 的最小值是________________;
的最小值是________________;
②函数![]() 的图象与函数
的图象与函数![]() 的图象的交点表示的含义是________________;
的图象的交点表示的含义是________________;
③若![]() ,AP的长约为________________cm
,AP的长约为________________cm
查看答案和解析>>
科目: 来源: 题型:
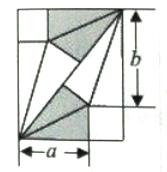
【题目】我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理,如图所示的长方形由两个这样的图形拼成,若![]() ,
,![]() ,则该长方形的面积为__________.
,则该长方形的面积为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】四边形ABCD是正方形,AC是对角线,E是平面内一点,且![]() ,过点C作
,过点C作![]() ,且
,且![]() 。连接AE、AF,M是AF的中点,作射线DM交AE于点N.
。连接AE、AF,M是AF的中点,作射线DM交AE于点N.
(1)如图1,若点E,F分别在BC,CD边上。
求证:①![]() ;
;
②![]() ;
;
(2)如图2,若点E在四边形ABCD内,点F在直线BC的上方,求![]() 与
与![]() 的和的度数。
的和的度数。

查看答案和解析>>
科目: 来源: 题型:
【题目】树叶有关的问题
如图,一片树叶的长是指沿叶脉方向量出的最长部分的长度(不含叶柄),树叶的宽是指沿与主叶脉垂直方向量出的最宽处的长度,树叶的长宽比是指树叶的长与树叶的宽的比值。

某同学在校园内随机收集了A树、B树、C树三棵的树叶各10片,通过测量得到这些树叶的长y(单位:cm),宽x(单位:cm)的数据,计算长宽比,理如下:
表1 A树、B树、C树树叶的长宽比统计表
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
A树树叶的长宽比 | 4.0 | 4.9 | 5.2 | 4.1 | 5.7 | 8.5 | 7.9 | 6.3 | 7.7 | 7.9 |
B树树叶的长宽比 | 2.5 | 2.4 | 2.2 | 2.3 | 2.0 | 1.9 | 2.3 | 2.0 | 1.9 | 2.0 |
C树树叶的长宽比 | 1.1 | 1.2 | 1.2 | 0.9 | 1.0 | 1.0 | 1.1 | 0.9 | 1.0 | 1.3 |
表1 A树、B树、C树树叶的长宽比的平均数、中位数、众数、方差统计表
平均数 | 中位数 | 众数 | 方差 | |
A树树叶的长宽比 | 6.2 | 6.0 | 7.9 | 2.5 |
B树树叶的长宽比 | 2.2 | 0.38 | ||
C树树叶的长宽比 | 1.1 | 1.1 | 1.0 | 0.02 |
A树、B树、C树树叶的长随变化的情况

解决下列问题:
(1)将表2补充完整;
(2)①小张同学说:“根据以上信息,我能判断C树树叶的长、宽近似相等。”
②小李同学说:“从树叶的长宽比的平均数来看,我认为,下图的树叶是B树的树叶。”
![]()
请你判断上面两位同学的说法中,谁的说法是合理的,谁的说法是不合理的,并给出你的理由;
(3)现有一片长103cm,宽52cm的树叶,请将该树叶的数用“★”表示在图1中,判断这片树叶更可能来自于A、B、C中的哪棵树?并给出你的理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,点P在函数![]() 的图象上,过P作直线
的图象上,过P作直线![]() 轴于点A,交直线
轴于点A,交直线![]() 于点M,过M作直线
于点M,过M作直线![]() 轴于点B.交函数
轴于点B.交函数![]() 的图象于点Q。
的图象于点Q。
(1)若点P的横坐标为1,写出点P的纵坐标,以及点M的坐标;
(2)若点P的横坐标为t,
①求点Q的坐标(用含t的式子表示)
②直接写出线段PQ的长(用含t的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com