
科目: 来源: 题型:
【题目】某工厂计划生产![]() 两种产品共60件,需购买甲、乙两种材料.生产一件
两种产品共60件,需购买甲、乙两种材料.生产一件![]() 产品需甲种材料4千克;生产一件
产品需甲种材料4千克;生产一件![]() 产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产![]() 产品不少于38件,问符合生产条件的生产方案有哪几种?
产品不少于38件,问符合生产条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件![]() 产品需加工费40元,生产一件
产品需加工费40元,生产一件![]() 产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低(成本=材料费+加工费)?
产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低(成本=材料费+加工费)?
查看答案和解析>>
科目: 来源: 题型:
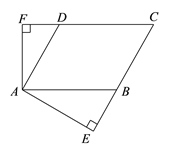
【题目】如图7,已知平行四边形ABCD的周长是32cm,AB︰BC=5︰3,AE⊥BC,垂足为E,AF⊥CD,垂足为F,∠EAF=2∠C.
(1)求∠C的度数;
(2)已知DF的长是关于![]() 的方程
的方程![]() -
-![]() -6=0的一个根,求该方程的另一个根.
-6=0的一个根,求该方程的另一个根.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本题满分12分)已知,直线AP是过正方形ABCD顶点A的任一条直线(不过B、C、D三点),点B关于直线AP的对称点为E,连结AE、BE、DE,直线DE交直线AP于点F.
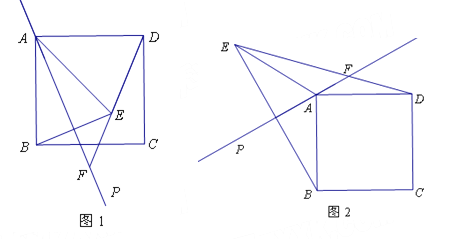
(1)如图1,直线AP与边BC相交.
①若∠PAB=20°,则∠ADF= °,∠BEF= °;
②请用等式表示线段AB、DF、EF之间的数量关系,并说明理由;
(2)如图2,直线AP在正方形ABCD的外部,且![]() ,
,![]() ,求线段AF的长.
,求线段AF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图6,在平面直角坐标系中,一次函数![]() =
=![]() +1的图象交
+1的图象交![]() 轴于点D,与反比例函数
轴于点D,与反比例函数![]() =
=![]() 的图象在第一象限相交于点A.过点A分别作
的图象在第一象限相交于点A.过点A分别作![]() 轴
轴![]() 轴的垂线,垂足为点BC.
轴的垂线,垂足为点BC.
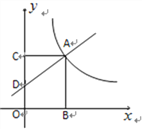
(1)点D的坐标为 ;
(2)当AB=4AC时,求![]() 值;
值;
(3)当四边形OBAC是正方形时,直接写出四边形ABOD与△ACD面积的比.
查看答案和解析>>
科目: 来源: 题型:
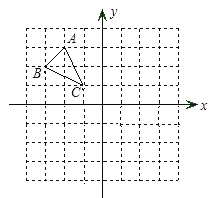
【题目】已知ABC 在平面直角坐标系中的位置如图(注: A、B、C 均在格点上)
(1)请在图中作出ABC 关于 y 轴对称的A1B1C1 ,并直接写出A1B1C1 顶点的坐标;
(2)求A1B1C1 的面积;
(3)再将A1B1C1 向下平移 4 个单位长度,得到A2 B2C2 ,若点 M m, n 是ABC 上一点,请直接写出 M 在A2 B2C2 上对应点 M 2 的坐标。
查看答案和解析>>
科目: 来源: 题型:
【题目】建设银行的某储蓄员小张在办理业务时,约定存入为正,取出为负. 2019年10月29日,他先后办理了七笔业务: +2000元、-800元、+400元、-800元、+1400元、-1700元、-200元.
(1)若他早上领取备用金4000元,那么下班时应交回银行_________元钱.
(2)请判断在这七次办理业务中,小张在第_______次业务办理后手中现金最多,第_________次业务办理后手中现金最少.
(3)若每办一件业务,银行发给业务量的0.2%作为奖励,小张这天应得奖金多少元?
(4)若记小张第一次办理业务前的现金为0点,用折线统计图表示这7次业务办理中小张手中现金的变化情况.

查看答案和解析>>
科目: 来源: 题型:
【题目】为积极响应市委政府“加快建设天蓝水碧地绿的美丽长沙”的号召,我市某街道决定从备选的五种树中选购一种进行栽种.为了更好地了解社情民意,工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图两个不完整的统计图:

请根据所给信息解答以下问题:
(1)这次参与调查的居民人数为: ;
(2)请将条形统计图补充完整;
(3)请计算扇形统计图中“枫树”所在扇形的圆心角度数;
(4)已知该街道辖区内现有居民8万人,请你估计这8万人中最喜欢玉兰树的有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】某市设计的长方形休闲广场如图所示,两端是两个半圆形的花坛,中间是一个直径为长方形宽度一半的圆形喷水池.
(1)用图中所标字母表示广场空地(图中阴影部分)的面积.
(2)若休闲广场的长为90米,宽为40米,求广场空地的面积(计算结果保留π).

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点O为直线AB上一点,过点O作直线OC,已知∠AOC≠90°,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE.

(1)求∠DOE和∠DOF的度数;
(2)若∠DOC=3∠COF,求∠AOC的度数;
(3)求∠BOF+∠DOC的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】我市某中学教务处为了了解该校学生的课外体育活动情况,对学生进行了随机的调查,分别从足球、篮球、乒乓球、羽毛球四个方面进行了汇总,然后将结果制成了如下的两幅不完整的统计图,请你根据统计图中提供的信息,解答下列问题:
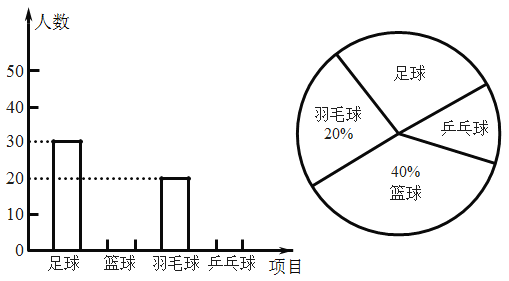
(1)在这次调查中,一共调查了多少名学生?
(2)在扇形统计图中,乒乓球项目所对的圆心角是多少度?
(3)请补充完整条形统计图.
(4)假如你是该校的一名学生,请你根据调查的结论,谈谈对于运动场所配置的建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com