
科目: 来源: 题型:
【题目】如图,在△ABC中,∠![]() =90°,
=90°,![]() =
=![]() =6,点
=6,点![]() 在边
在边![]() 上运动,过点
上运动,过点![]() 作
作![]() ⊥
⊥![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为邻边作□
为邻边作□![]() ,设□
,设□![]() 与△
与△![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,线段
,线段![]() 的长为
的长为![]() (0<
(0<![]() ≤6).
≤6).
(1)求线段![]() 的长(用含
的长(用含![]() 的代数式表示)
的代数式表示)
(2)当点![]() 落现在变
落现在变![]() 上时,求
上时,求![]() 的值;
的值;
(3)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)直接写出点![]() 到△
到△![]() 任意两边所在直线的距离相等时
任意两边所在直线的距离相等时![]() 的值.
的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知∠A=∠D=90°,点E、F在线段BC上,DE与AF交于点O,且AB=DC,BE=CF.求证:
(1)AF=DE
(2)若OP⊥EF,求证:OP平分∠EOF.
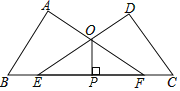
查看答案和解析>>
科目: 来源: 题型:
【题目】若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.

(1)已知△ABC是比例三角形,AB=2,BC=3,请直接写出所有满足条件的AC的长;
(2)如图1,在四边形ABCD中,AD∥BC,对角线BD平分∠ABC,∠BAC=∠ADC.
①求证:△ABC∽△DCA;②求证:△ABC是比例三角形;
(3)如图2,在(2)的条件下,当∠ADC=90°时,求出![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】直线y=x+b与双曲线y=![]() 交于点A(﹣1,﹣5).并分别与x轴、y轴交于点C、B.
交于点A(﹣1,﹣5).并分别与x轴、y轴交于点C、B.

(1)直接写出b= ,m= ;
(2)根据图象直接写出不等式x+b<![]() 的解集为 ;
的解集为 ;
(3)若点D在x轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在,请求出D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,如图,A、B分别为数轴上的两点,A点对应的数为-20,B点对应的数为100.
![]()
请写出AB中点M对应的数。
(2)现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动。设两只电子蚂蚁在数轴上的C点相遇,你知道C点对应的数是多少吗?
(3)若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动。设两只电子蚂蚁在数轴上的D点相遇,你知道D点对应的数是多少吗?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (1,0)和点
(1,0)和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,对称轴为直线
,对称轴为直线![]() =1.
=1.
(1)求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示)
的代数式表示)
(2)连接![]() 、
、![]() ,若△
,若△![]() 的面积为6,求此抛物线的解析式;
的面积为6,求此抛物线的解析式;
(3)在(2)的条件下,点![]() 为
为![]() 轴正半轴上的一点,点
轴正半轴上的一点,点![]() 与点
与点![]() ,点
,点![]() 与点
与点![]() 关于点
关于点![]() 成中心对称,当△
成中心对称,当△![]() 为直角三角形时,求点
为直角三角形时,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】某同学模仿二维码的方式为学校设计了一个身份识别图案系统:在![]() 的正方形网格中,黑色正方形表示数字1,白色正方形表示数字0.如图1是某个学生的身份识别图案.约定如下:把第i行,第j列表示的数字记为
的正方形网格中,黑色正方形表示数字1,白色正方形表示数字0.如图1是某个学生的身份识别图案.约定如下:把第i行,第j列表示的数字记为![]() (其中i,j=1,2,3,4),如图1中第2行第1列的数字
(其中i,j=1,2,3,4),如图1中第2行第1列的数字![]() =0;对第i行使用公式
=0;对第i行使用公式![]() 进行计算,所得结果
进行计算,所得结果![]() 表示所在年级,
表示所在年级,![]() 表示所在班级,
表示所在班级,![]() 表示学号的十位数字,
表示学号的十位数字,![]() 表示学号的个位数字.如图1中,第二行
表示学号的个位数字.如图1中,第二行![]() ,说明这个学生在5班.
,说明这个学生在5班.
(1)图1代表的学生所在年级是______年级,他的学号是_________;
(2)请仿照图1,在图2中画出八年级4班学号是36的同学的身份识别图案

查看答案和解析>>
科目: 来源: 题型:
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.

(1)求证:△OCP∽△PDA;
(2)若△OCP与△PDA的面积比为1:4,①求边CP的长;②求边AB的长;
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)观察下列各式:
![]() ……试用你发现的规律填空:
……试用你发现的规律填空:![]() ,
,![]() 。
。
(2)请你用含有一个字母的等式将上面各式呈现的规律表示出来,并用所学数学知识说明你所写式子的正确性。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com