
科目: 来源: 题型:
【题目】某次水灾导致大约有![]() 人无家可归,假如一顶帐篷占地
人无家可归,假如一顶帐篷占地![]() ,可以放置40个单人床位.
,可以放置40个单人床位.
(1)为了安置所有无家可归的人,需要多少顶帐篷?这些帐篷大约要占多大地方?
(2)若学校的操场面积为![]() ,可安置多少人?
,可安置多少人?
(3)要安置所有无家可归的人,大约需要多少个这样的操场?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,甲和乙同时从学校放学,两人以各自送度匀速步行回家,甲的家在学校的正西方向,乙的家在学校的正东方向,乙家离学校的距离比甲家离学校的距离远3900米,甲准备一回家就开始做什业,打开书包时发现错拿了乙的练习册.于是立即步去追乙,终于在途中追上了乙并交还了练习册,然后再以先前的速度步行回家,(甲在家中耽搁和交还作业的时间忽略不计)结果甲比乙晚回到家中,如图是两人之间的距离y米与他们从学校出发的时间x分钟的函数关系图,则甲的家和乙的家相距_____米.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 第一象限内的图象相交于点
第一象限内的图象相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
(2)观察反比例函数![]() 的图象,当
的图象,当![]() 时,请直接写出
时,请直接写出![]() 的取值范围;
的取值范围;
(3)如图,以![]() 为边作菱形
为边作菱形![]() ,使点
,使点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在第一象限,双曲线交
在第一象限,双曲线交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,求
,求![]() .
.

查看答案和解析>>
科目: 来源: 题型:
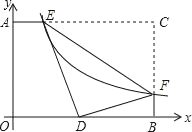
【题目】如图,在矩形AOBC中,OB=4,OA=3,分别以OB,OA所在直线为x轴、y轴建立平面直角坐标系,F是BC边上的点,过F点的反比例函数y=![]() (k>0)的图象与AC边交于点E.若将△CEF沿EF翻折后,点C恰好落在OB上的点D处,则点F的坐标为_____.
(k>0)的图象与AC边交于点E.若将△CEF沿EF翻折后,点C恰好落在OB上的点D处,则点F的坐标为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )
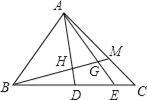
A. 3:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
查看答案和解析>>
科目: 来源: 题型:
【题目】若一组数据x1 , x2 , x3 , x4 , x5 , x6的平均数是2,方差是2,则另一组数据3x1-2 , 3x2-2 , 3x3-2 , 3x4-2 , 3x5-2 , 3x6-2的平均数和方差分别是( ).
A.2, 2 B.2, 18 C.4, 6 D.4, 18
查看答案和解析>>
科目: 来源: 题型:
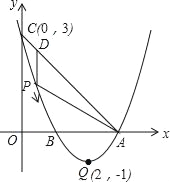
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,﹣1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
(1)求该抛物线的函数关系式;
(2)当△ADP是直角三角形时,求点P的坐标;
(3)在题(2)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】一辆出租车从![]() 地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下表所示(
地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下表所示(![]() ,单位:
,单位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 |
|
|
|
|
(1)写出这辆出租车每次行驶的方向.
(2)求经过连续4次行驶后,这辆出租车所在的位置.
(3)这辆出租车一共行驶多少路程?
查看答案和解析>>
科目: 来源: 题型:
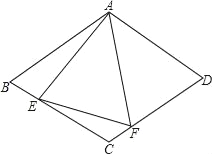
【题目】如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形的边BC,CD上.
(1)证明:BE=CF.
(2)当点E,F分别在边BC,CD上移动时(△AEF保持为正三角形),请探究四边形AECF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
(3)在(2)的情况下,请探究△CEF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市区自2014年1月起,居民生活用水开始实行阶梯式计量水价,该阶梯式计量水价分为三级(如下表所示):
月用水量(吨) | 水价(元/吨) |
第一级 20吨以下(含20吨) | 1.6 |
第二级 20吨﹣30吨(含30吨) | 2.4 |
第三级 30吨以上 | 3.2 |
例:某用户的月用水量为32吨,按三级计量应缴水费为:
1.6×20+2.4×10+3.2×2=62.4(元)
(1)如果甲用户的月用水量为12吨,则甲需缴的水费为 元;
(2)如果乙用户缴的水费为39.2元,则乙月用水量 吨;
(3)如果丙用户的月用水量为a吨,则丙用户该月应缴水费多少元?(用含a的代数式表示,并化简)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com