
科目: 来源: 题型:
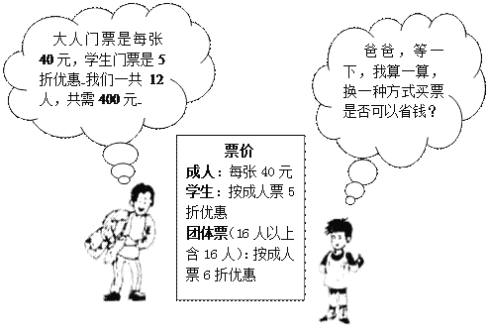
【题目】暑假期间,七(2)班的张明、王强等同学随家长一同到某公园游玩,下面是购买门票时,张明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
⑴ 张明他们一共去了几个成人,几个学生?
⑵ 请你帮助张明算一算,用哪种方式购票(团体购票还是非团体购票)更省钱?
说明理由.
⑶ 正要购票时,张明发现七(3)班的张小毛等15名同学和他们的2名家长共17人也来购票,请你为他们设计出最省的购票方案,并求出此时的购票费用.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得![]() ≌
≌![]() 即可得
即可得![]() ,则可证得
,则可证得![]() 为
为![]() 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得![]() 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得![]() 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得![]() 与
与![]() 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
试题解析:(1)证明:连接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切线;
的切线;
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直径,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面积为![]()

【题型】解答题
【结束】
25
【题目】【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E.
(1)∠ACB= °,理由是: ;
(2)猜想△EAD的形状,并证明你的猜想;
(3)若AB=8,AD=6,求BD.

查看答案和解析>>
科目: 来源: 题型:
【题目】小明是个爱动脑筋的同学,在发现教材中的用方框在月历中移动的规律后,突发奇想,将连续的偶数2,4,6,8,…,排成如图:并用一个十字形框架框住其中的五个数,请你仔细观察十字形框架中的数字的规律,并回答下列问题:
(1)十字框中的五个数的和与中间的数16有什么关系?
(2)设中间的数为x,用代数式表示十字框中的五个数的和;
(3)若将十字框上下左右移动,可框住另外的五位数,其它五位数的和能等于2015吗?如能,写出这五位数,如不能,说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的方程![]() =x+
=x+![]() 与
与![]() =6x﹣2的解互为倒数,
=6x﹣2的解互为倒数,
(1)求m的值.
(2)若当y=m时,代数式ay3+by+1的值为5,求当y=﹣m时,代数式ay3+by+1的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,第一象限内的点A、B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且tan∠ACB=![]()
求:(1)反比例函数的解析式;
(2)点C的坐标;
(3)sin∠ABC的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

查看答案和解析>>
科目: 来源: 题型:
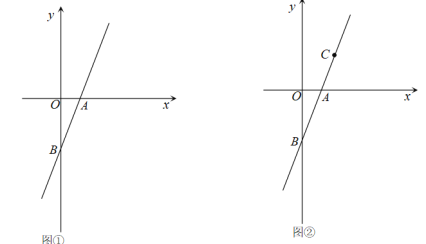
【题目】已知,直线y=2x-2与x轴交于点A,与y轴交于点B.
(1)如图①,点A的坐标为_______,点B的坐标为_______;
(2)如图②,点C是直线AB上不同于点B的点,且CA=AB.
①求点C的坐标;
②过动点P(m,0)且垂直与x轴的直线与直线AB交于点E,若点E不在线段BC上,则m的取值范围是_______;
(3)若∠ABN=45,求直线BN的解析式.
查看答案和解析>>
科目: 来源: 题型:
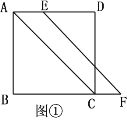
【题目】已知,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,且AE=CF,连接AC,EF.
(1)如图①,求证:EF//AC;
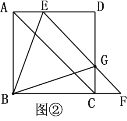
(2)如图②,EF与边CD交于点G,连接BG,BE,
①求证:△BAE≌△BCG;
②若BE=EG=4,求△BAE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com