
科目: 来源: 题型:
【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.分析甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分钟)变化的函数图象,解决下列问题:

(1)求出甲、乙两人所行驶的路程S甲、S乙与t之间的关系式;
(2)甲行驶15分钟后,甲、乙两人相距多少千米?
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料:我们知道,分数可分为“真分数”和“假分数”,而假分数都可化为带分数,如![]() 我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”,当分子的次数小于分母的次数时,我们称之为“真分式”,如
我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”,当分子的次数小于分母的次数时,我们称之为“真分式”,如![]() 这样的分式就是假分式;再如:
这样的分式就是假分式;再如:![]() 这样的分式就是真分式。类似的,假分式也可以化为带分式(即:整式与真分式的和的形式),如:
这样的分式就是真分式。类似的,假分式也可以化为带分式(即:整式与真分式的和的形式),如:
![]()
请解决下列问题:
(1)分式![]() 是_____分式(填“真”或“假”);
是_____分式(填“真”或“假”);
(2)将假分式![]() 化为带分式;
化为带分式;
(3)若分式![]() 的值为整数,直接写出所有符合条件的正整数
的值为整数,直接写出所有符合条件的正整数![]() 的值。
的值。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知一次函数![]() 与反比例函数
与反比例函数![]() 的图象在第一、第三象限分别交于
的图象在第一、第三象限分别交于![]() ,
,![]() 两点,直线
两点,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点.
两点.
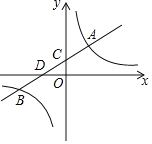
(1)求一次函数和反比例函数的解析式;
(2)比较大小:![]()
![]() ;
;
(3)求出![]() 时,
时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于钝角α,定义它的三角函数值如下:
sinα=sin(180°﹣α),cosα=﹣cos(180°﹣α)
(1)求sin120°,cos120°,sin150°的值;
(2)若一个三角形的三个内角的比是1:1:4,A,B是这个三角形的两个顶点,sinA,cosB是方程4x2﹣mx﹣1=0的两个不相等的实数根,求m的值及∠A和∠B的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,规定:抛物线y=a(xh) ![]() +k的关联直线为y=a(xh)+k.
+k的关联直线为y=a(xh)+k.
例如:抛物线y=2(x+1) ![]() 3的关联直线为y=2(x+1)3,即y=2x1.
3的关联直线为y=2(x+1)3,即y=2x1.
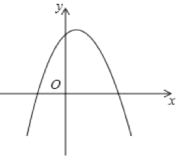
(1)如图,对于抛物线y=(x1) ![]() +3.
+3.
①该抛物线的顶点坐标为___,关联直线为___,该抛物线与其关联直线的交点坐标为___和___;
②点P是抛物线y=(x1) ![]() +3上一点,过点P的直线PQ垂直于x轴,交抛物线y=(x1)
+3上一点,过点P的直线PQ垂直于x轴,交抛物线y=(x1)![]() +3的关联直线于点Q.设点P的横坐标为m,线段PQ的长度为d(d>0),求当d随m的增大而减小时,d与m之间的函数关系式,并写出自变量m的取值范围。
+3的关联直线于点Q.设点P的横坐标为m,线段PQ的长度为d(d>0),求当d随m的增大而减小时,d与m之间的函数关系式,并写出自变量m的取值范围。
(2)顶点在第一象限的抛物线y=a(x1) ![]() +4a与其关联直线交于点A,B(点A在点B的左侧),与x轴负半轴交于点C,直线AB与x轴交于点D,连结AC、BC.
+4a与其关联直线交于点A,B(点A在点B的左侧),与x轴负半轴交于点C,直线AB与x轴交于点D,连结AC、BC.
①求△BCD的面积(用含a的代数式表示).
②当△ABC为钝角三角形时,直接写出a的取值范围。
查看答案和解析>>
科目: 来源: 题型:
【题目】外卖小哥骑车从商家出发,向东骑了3千米到达小林家,继续骑2.5千米到达小红家,然后向西骑了10千米到达小明家,最后返回商家。
(1)以商家为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家,小林家,小红家的位置。(小林家用点A表示,小红家用点B表示,小明家用点C表示)
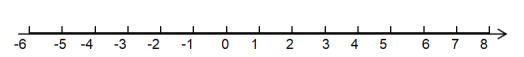
(2)小明家距小林家______千米
(3)若外卖小哥在骑车过程中每千米耗时3分钟,那么外卖小哥在整个过程中共用时多久?(假设外卖小哥一直在匀速行驶,在每户人家上门送外卖的时间忽略不计)
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料:
数学课上,老师出示了这样一个问题:
如图,菱形![]() 和四边形
和四边形![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
求证:![]() ;
;
某学习小组的同学经过思考,交流了自己的想法:
小明:“通过观察分析,发现![]() 与
与![]() 存在某种数量关系”;
存在某种数量关系”;
小强:“通过观察分析,发现图中有等腰三角形”;
小伟:“利用等腰三角形的性质就可以推导出![]() ”.
”.
……
老师:“将原题中的条件‘![]() ’与结论‘
’与结论‘![]() ’互换,即若
’互换,即若![]() ,则
,则![]() ,其它条件不变,即可得到一个新命题”.
,其它条件不变,即可得到一个新命题”.
……
请回答:
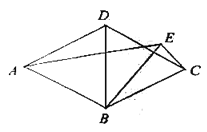
(1)在图中找出与线段![]() 相关的等腰三角形(找出一个即可),并说明理由;
相关的等腰三角形(找出一个即可),并说明理由;
(2)求证:![]() ;
;
(3)若![]() ,则
,则![]() 是否成立?若成立,请证明;若不成立,请说明理由.
是否成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校在一次大课间活动中,采用了四钟活动形式:A、跑步,B、跳绳,C、做操,D、游戏.全校学生都选择了一种形式参与活动,小杰对同学们选用的活动形式进行了随机抽样调查,根据调查统计结果,绘制了不完整的统计图.


请结合统计图,回答下列问题:
(1)本次调查学生共 人, ![]() = ,并将条形图补充完整;
= ,并将条形图补充完整;
(2)如果该校有学生2000人,请你估计该校选择“跑步”这种活动的学生约有多少人?
(3)学校让每班在A、B、C、D四钟活动形式中,随机抽取两种开展活动,请用树状图或列表的方法,求每班抽取的两种形式恰好是“跑步”和“跳绳”的概率.
查看答案和解析>>
科目: 来源: 题型:
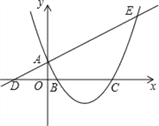
【题目】如图,已知直线y=![]() x+1与y轴交于点A,与x轴交于点D,抛物线y=
x+1与y轴交于点A,与x轴交于点D,抛物线y= ![]() x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).在抛物线的对称轴上找一点M,使|AM﹣MC|的值最大,求出点M的坐标__________.
x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).在抛物线的对称轴上找一点M,使|AM﹣MC|的值最大,求出点M的坐标__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com