
科目: 来源: 题型:
【题目】如图,已知直线![]() 与反比例函数
与反比例函数![]() 的图象交于点A(2,
的图象交于点A(2,![]() );将直线
);将直线![]() 向下平移后与反比例函数
向下平移后与反比例函数![]() 的图象交于点B,且△AOB的面积为3.
的图象交于点B,且△AOB的面积为3.
(1)求![]() 的值;
的值;
(2)求平移后所得直线的函数表达式.

查看答案和解析>>
科目: 来源: 题型:
【题目】在一条不完整的数轴上从左到右有点A,B,C,其中点A到点B的距离为3,点C到点B的距离为7,如图所示:设点A,B,C所对应的数的和是m.
![]()
(1)若以C为原点,则m的值是_______;
(2)若原点0在图中数轴上,且点C到原点0的距离为4,求m的值;
(3)动点P从A点出发,以每秒2个单位长度的速度向终点C移动,动点Q同时从B点出发,以每秒1个单位的速度向终点C移动,当几秒后,P、Q两点间的距离为2?(直接写出答案即可)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,图中四个直角三角形是全等的,若大正方形ABCD的面积是小正方形EFGH面积的13倍,则![]() 的值为______________.
的值为______________.

查看答案和解析>>
科目: 来源: 题型:
【题目】将正方形 ABCD (如图 1)作如下划分:
第1次划分:分别连接正方形ABCD对边的中点(如图2),得线段HF和EG,它们交于点M,此时图2中共有5个正方形;
第2次划分:将图2 左上角正方形AEMH再作划分,得图3,则图3 中共有9个正方形;
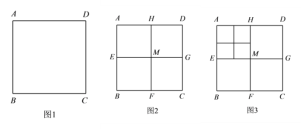
(1)若每次都把左上角的正方形依次划分下去,则第100次划分后,图中共有 个正方形;
(2)继续划分下去,第几次划分后能有805个正方形?写出计算过程.
(3)按这种方法能否将正方形ABCD划分成有2015个正方形的图形?如果能,请算出是第几次划分,如果不能,需说明理由.
(4)如果设原正方形的边长为1,通过不断地分割该面积为1的正方形,并把数量关系和几何图形巧妙地结合起来,可以很容易得到一些计算结果,试着探究求出下面表达式的结果吧.
计算 ![]() .( 直接写出答案即可)
.( 直接写出答案即可)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是某种产品展开图,高为3cm.
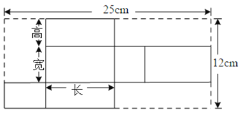
(1)求这个产品的体积.
(2)请为厂家设计一种包装纸箱,使每箱能装5件这种产品,要求没有空隙且要使该纸箱所用材料尽可能少(纸的厚度不计,纸箱的表面积尽可能小),求此长方体的表面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
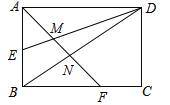
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】知识再现:
如果![]() ,
,![]() ,则线段
,则线段![]() 的中点坐标为
的中点坐标为![]() ;对于两个一次函数
;对于两个一次函数![]() 和
和![]() ,若两个一次函数图象平行,则
,若两个一次函数图象平行,则![]() 且
且![]() ;若两个一次函数图象垂直,则
;若两个一次函数图象垂直,则![]() .
.
提醒:在下面这个相关问题中如果需要,你可以直接利用以上知识.
在平面直角坐标系中,已知点![]() ,
,![]() .
.
(1)如图1,把直线![]() 向右平移使它经过点
向右平移使它经过点![]() ,如果平移后的直线交
,如果平移后的直线交![]() 轴于点
轴于点![]() ,交x轴于点
,交x轴于点![]() ,请确定直线
,请确定直线![]() 的解析式.
的解析式.
(2)如图2,连接![]() ,求
,求![]() 的长.
的长.
(3)已知点![]() 是直线
是直线![]() 上一个动点,以
上一个动点,以![]() 为对角线的四边形
为对角线的四边形![]() 是平行四边形,当
是平行四边形,当![]() 取最小值时,请在图3中画出满足条件的
取最小值时,请在图3中画出满足条件的![]() ,并直接写出此时
,并直接写出此时![]() 点坐标.
点坐标.
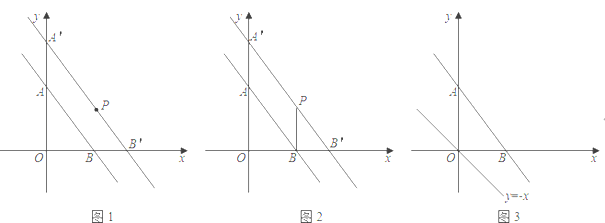
查看答案和解析>>
科目: 来源: 题型:
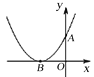
【题目】如图,已知二次函数![]() 的图象与y轴的正半轴交于点A,其顶点B在
的图象与y轴的正半轴交于点A,其顶点B在![]() 轴的负半轴上,且OA=OB,对于下列结论:①
轴的负半轴上,且OA=OB,对于下列结论:①![]() ≥0;②
≥0;②![]() ;③关于
;③关于![]() 的方程
的方程![]() 无实数根;④
无实数根;④![]() 的最小值为3.其中正确结论的个数为( )
的最小值为3.其中正确结论的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
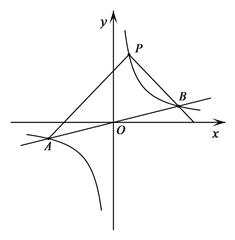
【题目】如图,反比例函数y=![]() 的图象与一次函数y=
的图象与一次函数y=![]() x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
(1)若点P的坐标是(1,4),直接写出k的值和△PAB的面积;
(2)设直线PA、PB与x轴分别交于点M、N,求证:△PMN是等腰三角形;
(3)设点Q是反比例函数图象上位于P、B之间的动点(与点P、B不重合),连接AQ、BQ,比较∠PAQ与∠PBQ的大小,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(知识背景)
据我国古代《周髀算经》记载,公元前1120年商高对周公说,将一根直尺折成一个直角,两端连接得到一个直角三角形,如果勾是3,股是4,那么弦就等于5,后人概括为“勾三、股四、弦五”.像3、4、5这样为三边长能构成直角三角形的三个正整数,称为勾股数.
(应用举例)
观察3,4,5;5,12,13;7,24,25;…
可以发现这些勾股数的勾都是奇数,且从3起就没有间断过,并且
勾为3时,股![]() ,弦
,弦![]() ;
;
勾为5时,股![]() ,弦
,弦![]() ;
;
请仿照上面两组样例,用发现的规律填空:
(1)如果勾为7,则股24= 弦25=
(2)如果勾用![]() (
(![]() ,且
,且![]() 为奇数)表示时,请用含有
为奇数)表示时,请用含有![]() 的式子表示股和弦,则股= ,弦= .
的式子表示股和弦,则股= ,弦= .
(解决问题)
观察4,3,5;6,8,10;8,15,17;…根据应用举例获得的经验进行填空:
(3)如果![]() 是符合同样规律的一组勾股数,
是符合同样规律的一组勾股数,![]() (
(![]() 表示大于1的整数),则
表示大于1的整数),则![]() ,
,![]() ,这就是古希腊的哲学家柏拉图提出的构造勾股数组的公式.
,这就是古希腊的哲学家柏拉图提出的构造勾股数组的公式.
(4)请你利用柏拉图公式,补全下面两组勾股数(数据从小到大排列)第一组: 、24、 :第二组: 、 、37.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com