（1）如图1，若边BD，BA在同一直线上，则∠EBC= ；

（2）如图2，若∠EBC=165°，那么∠ABD= ；

（3）如图3，若∠EBC=120°，求∠ABD的度数。

（1）2x﹣3（x+2）＝5x﹣2（x﹣1）；

（2）﹣+1＝．

【题目】如图，直线和相交于点C，分别交x轴于点A和点B点P为射线BC上的一点。

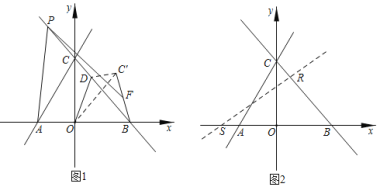
（1）如图1，点D是直线CB上一动点，连接OD，将沿OD翻折，点C的对应点为，连接，并取的中点F，连接PF，当四边形AOCP的面积等于时，求PF的最大值；

（2）如图2，将直线AC绕点O顺时针方向旋转α度，分别与x轴和直线BC相交于点S和点R，当是等腰三角形时，直接写出α的度数.

（1）求抛物线的解析式；

（2）已知点M为y轴上的一个动点，当△ABM为等腰三角形时，求点M的坐标；

（3）将△AOB沿x轴向右平移m个单位长度（0＜m＜3）得到另一个三角形，将所得的三角形与△ABC重叠部分的面积记为S，用m的代数式表示S，并求其最大值．

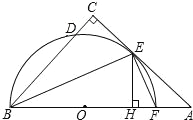
（1）求证：AC是⊙O的切线．

（2）过点E作EH⊥AB于点H，求证：CD=HF．

【题目】数形结合是一种重要的数学思想，我们不但可以用数来解决图形问题，同样也可以用借助图形来解决数量问题，往往能出奇制胜，数轴和勾股定理是数形结合的典范.数轴上的两点A和B所表示的数分别是和，则A，B两点之间的距离；坐标平面内两点，，它们之间的距离.如点，，则.表示点与点之间的距离，表示点与点和的距离之和.

（1）已知点，，________；

（2）表示点和点之间的距离；

（3）请借助图形，求的最小值.

（1）如图1，当∠MON的一边OM与射线OB重合时，则∠NOC=_________；

（2）将∠MON绕点O逆时针运动至图2时，若∠MOC=15°，则∠BOM=______；∠AON=_______.

（3）在上述∠MON从图1运动到图3的位置过程中，当∠MON的边OM所在直线恰好平分∠AOC时，求此时∠NOC是多少度？

【题目】八年级（1）班张山同学利用所学函数知识，对函数进行了如下研究：

列表如下：

描点并连线（如下图）

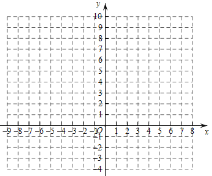
（1）自变量x的取值范围是________；

（2）表格中：________，________；

（3）在给出的坐标系中画出函数的图象；

（4）一次函数的图象与函数的图象交点的坐标为_______.

+150，﹣35，﹣42，﹣35，+128，﹣26，﹣5，+30，+75

（1）他们最终有没有登上顶峰？如果没有，那么他们离顶峰还差多少米？

（2）登山时，3名队员在进行全程中都使用了氧气，且每人每米要消耗氧气0.04升.他们共使用了氧气多少升？