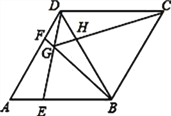
【题目】如图，在菱形ABCD中，AB=BD．点E、F分别在AB、AD上，且AE=DF．连接BF与DE相交于点G，连接CG与BD相交于点H．下列结论：①△AED≌△DFB； ②S四边形BCDG=CG2；③DE=CG；④若AF=2DF，则BG=6GF．其中正确的结论_____________．

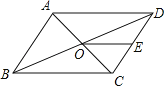
A. 15 B. 18 C. 21 D. 24

(1)如图1，当点P在线段AO上时，试猜想PE与PD的数量关系和位置关系，不用说明理由；

(2)如图2，当点P在线段OC上时，(1)中的猜想还成立吗？请说明理由；

(3)如图3，当点P在AC的延长线上时，请你在图3中画出相应的图形(尺规作图，保留作图痕迹，不写作法)，并判断(1)中的猜想是否成立？若成立，请直接写出结论；若不成立，请说明理由．

（1）求证:CE=AD

（2）若D为AB的中点,则∠A的度数满足什么条件时,四边形BECD是正方形？请说明理由.

已知，如图，∠BAE+∠AED=180°，∠M=∠N，试说明：∠1=∠2．

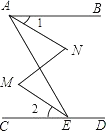
解：∵∠BAE+∠AED=180°

∴ AB∥CD（ ）

∴∠BAE=　　　　　　（ ）

又∵∠M=∠N （已知）

∴ AN∥　　　　　　（ ）

∴∠NAE=　　　　　　（两直线平行，内错角相等）

∴∠BAE﹣∠NAE=　　　　　　﹣　　　　　　

即∠1=∠2.（ ）

A. 2π B. 4π C. D. 4

（1）求证：AB=CF；

（2）连接DE，若AD=2AB，求证：DE⊥AF．

【题目】定义：当点C在线段AB上，AC=nAB时，我们称n为点C在线段AB上的点值，记作dC﹣AB=n．如点C是AB的中点时，即AC=AB，则dC﹣AB=；反过来，当dC﹣AB=时，则有AC=AB．

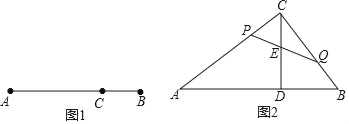
（1）如图1，点C在线段AB上，若dC﹣AB=，则=　 　；若AC=3BC，则dC﹣AB=　 　；

（2）如图2，在△ABC中，∠ACB=90°，CD⊥AB于点D，AB=10cm，BC=6cm，点P、Q分别从点C和点B同时出发，点P沿线段CA以2cm/s的速度向点A运动，点Q沿线段BC以1cm/s的速度向点C运动，当点P到达点A时，点P、Q均停止运动，连接PQ交CD于点E，设运动时间为ts，dP﹣CA+dQ﹣CB=m．

①当≤m≤时，求t的取值范围；

②当dP﹣CA=，求dE﹣CD的值；

③当dE﹣CD=时，求t的值．

表一：

（1）根据表一的信息，请在表二中填写滚动的距离s（单位：米）的对应值，（提示：本题中，s=×x， =，其中，v0表示开始时的速度，vx表示x秒时的速度．）

表二：

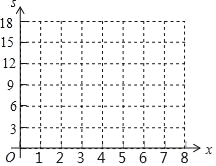
（2）根据表二中的数据在给出的平面坐标系中画出相应的点；

（3）选择适当的函数表示s与x之间的关系，求出相应的函数解析式；

（4span>）当s=13.75时，求滚动时间x．

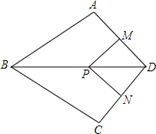
（1）求证：ADB=CDB；

（2）若ADC=90°，求证：四边形MPND是正方形。