
科目: 来源: 题型:
【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
查看答案和解析>>
科目: 来源: 题型:
【题目】有大小两种货车,2辆大货车与3辆小货车一次可以运货15.5吨,5辆大货车与6辆小货车一次可以运货35吨.
(1)每辆大货车和每辆小货车一次各可以运货多少吨?
(2)现在租用这两种货车共10辆,要求一次运输货物不低于30吨,则大货车至少租几辆?
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解某地区5000名九年级学生体育成绩状况,随机抽取了若干名学生进行测试,将成绩按A,B,C,D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:


(1)在这次抽样调查中,一共抽取了______名学生;
(2)请把条形统计图补充完整;
(3)请估计该地区九年级学生体育成绩为B级的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,ΔABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
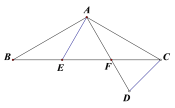
(1)求证:ΔABE≌ΔACF;
(2)若∠BAE=30°,则∠ADC= (直接写答案)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AD是⊙O的直径,AD=12,点B、C在⊙O上,AB、DC的延长线交于点E,且CB=CE,∠BCE=70°.

有以下结论:①∠ADE=∠E;②劣弧![]() 的长为
的长为![]() ;③点C为
;③点C为![]() 的中点;④BD平分∠ADE.以上结论一定正确的是_________________.(把正确结论的序号都填上)
的中点;④BD平分∠ADE.以上结论一定正确的是_________________.(把正确结论的序号都填上)
【答案】①②③
【解析】分析:①根据内接四边形的对角互补得到∠CBE=∠ADE,根据等腰三角形的性质得到∠CBE=∠E,即可证明.
②求出圆心角的度数,根据弧长公式求解即可.
③证明∠DAC=∠EAC,即可证明.
④∠A≠∠E,BD不平分∠ADE.
详解:①∠CBE为圆内接四边形ABCD的外角,则∠CBE=∠ADE,
CB=CE,所以∠CBE=∠E,因此∠ADE=∠E.
②∠A=∠BCE=70°,∴∠AOB=40°,![]() 的长=
的长=![]()
③由题意知:AC⊥DE,由∠ADE=∠E得AD=AE,
∴∠DAC=∠EAC,∴点C为![]() 的中点.
的中点.
④DB⊥AE,而∠A≠∠E,∴BD不平分∠ADE. 正确结论①②③
故答案为:①②③.
点睛:属于圆的综合题,考查圆内接四边形的性质,圆周角定理,弧长公式等,考查知识点较多,对学生综合分析能力要求较高.
【题型】填空题
【结束】
15
【题目】计算:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】解不等式组: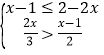 , 并把解集在数轴上表示出来.
, 并把解集在数轴上表示出来.
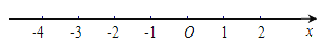
【答案】-3<x≤1
【解析】分析:分别解不等式,在数轴上表示出解集,找出解集的公共部分即可.
详解: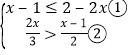 ,
,
解不等式①得:![]() ,
,
解不等式②得:![]()
∴原不等式组的解集为-3<x≤1
解集在数轴上表示为:

点睛:考查解一元一次不等式组,比较容易,分别解不等式,找出解集的公共部分即可.
【题型】解答题
【结束】
17
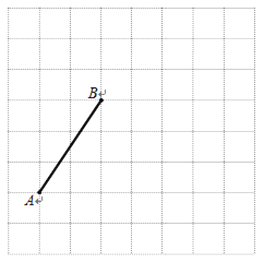
【题目】下图是由边长为1个单位长度的小正方形组成的网格,线段AB的端点在格点上.
(1)请建立适当的平面直角坐标系xOy,使得A点的坐标为(-3,-1),在此坐标系下,B点的坐标为________________;
(2)将线段BA绕点B逆时针旋转90°得线段BC,画出BC;在第(1)题的坐标系下,C点的坐标为__________________;
(3)在第(1)题的坐标系下,二次函数y=ax2+bx+c(a≠0)的图象过O、B、C三点,则此函数图象的对称轴方程是________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,以直线AB上一点O为端点作射线OC,使∠AOC=65°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OA上,则∠COE= ;
(2)如图②,将直角三角板DOE绕点O顺时针方向转动到某个位置,若OC恰好平分∠AOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O任意转动,如果OD始终在∠AOC的内部,试猜想∠AOD和∠COE有怎样的数量关系?并说明理由.

查看答案和解析>>
科目: 来源: 题型:
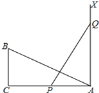
【题目】如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP= ______ .
查看答案和解析>>
科目: 来源: 题型:
【题目】把2018个正整数1,2,3,4,…,2018按如图方式排列成一个表.

(1)用如图方式框住表中任意4个数,记左上角的一个数为![]() ,则另三个数用含
,则另三个数用含![]() 的式子表示出来,从小到大依次是__________、___________、_______________(请直接填写答案);
的式子表示出来,从小到大依次是__________、___________、_______________(请直接填写答案);
(2)用(1)中方式被框住的4个数之和可能等于2019吗?如果可能,请求出![]() 的值;如果不可能,请说明理由.
的值;如果不可能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】下表是某水文站在雨季对某条河一周内水位变化情况的记录(上升为正,下降为负)
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
水位变化/ | +0.2 | +0.3 | -0.4 | -0.4 | -0.1 | +0.2 | +0.4 |
注:①表中记录的数据为每天中午12时的水位与前一天12时水位的变化量;②上星期日12时的水位高度为![]() .
.

(1)请你通过计算说明本周日与上周日相比,水位是上升了还是下降了;
(2)用折线连接本周每天的水位,并根据折线说明水位在本周内的升降趋势.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com