
科目: 来源: 题型:
【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片 ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB、 AC于点E、G.连接GF.则下列结论错误的是( )
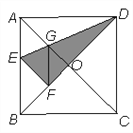
A. ∠AGD=112.5° B. 四边形AEFG是菱形 C. tan∠AED=2 D. BE=2OG
查看答案和解析>>
科目: 来源: 题型:
【题目】如图:在△ABC中,AB=5,AC=3,则BC边上的中线AD的取值范围是( ).
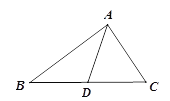
A. 2<AD<8B. 0<AD<8C. 1<AD<4D. 3<AD<5
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.根据两人的作法可判断( )
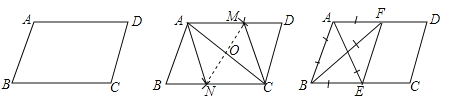
A. 甲正确,乙错误 B. 乙正确,甲错误
C. 甲、乙均正确 D. 甲、乙均错误
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在平面直角坐标系中,△AOB为等腰直角三角形,A(4,4).
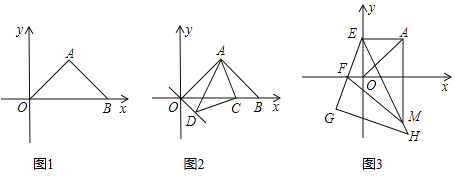
(1)点B坐标为
(2)如图2,若C为x轴正半轴上一动点,以AC为直角边作等腰Rt△ACD,∠ACD=90,连OD,求∠AOD的度数;
(3)如图3,过点A作y轴的垂线交y轴于点E,F为x轴负半轴上一点,点G在EF的延长线上,以EG为直角边作等腰Rt△EGH,过点A作x轴垂线交EH于点M,连FM,等式![]() =1是否成立?若成立,请证明;若不成立,说明理由.
=1是否成立?若成立,请证明;若不成立,说明理由.
查看答案和解析>>
科目: 来源: 题型:
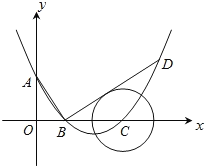
【题目】如图,在平面直角坐标系中,顶点为(4,1)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,3).
(1)求此抛物线的解析式;
(2)已知点P是抛物线上的一个动点,且位于A,C两点之间,问:当点P运动到什么位置时,△PAC的面积最大?并求出此时P点的坐标和△PAC的最大面积;
(3)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴![]() 与
与![]() 有怎样的位置关系,并给出证明.
有怎样的位置关系,并给出证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明在学习过程中遇到这样一个问题:如图1,在△ABC中,CA=CB,E是CD上一点,且ED=EB, ∠DEB=∠ACB,连接AD,探究∠ADC与∠DCB之间的数量关系.小明发现,∠ACD=∠CBE,CA=CB,因此可以通过作∠CAF=∠BCE交CD于点F构造全等,经过推理论证解决问题.
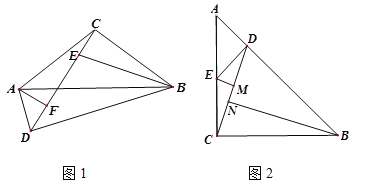
(1)按照小明思考问题的方法,解决问题;
(2)如图2,∠ACB=90,CA=CB,D是AB上一点,过点D作DE⊥AB交AC于点E,过点E作EM⊥CD于点M,BN⊥CD于点N,探究EM,BN,CD之间的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)出发2秒后,求PQ的长.
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.

查看答案和解析>>
科目: 来源: 题型:
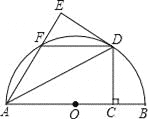
【题目】如图,AB是半圆O的直径,点C为半径OB上一点,过点C作CD丄AB交半圆O于点D,将△ACD沿AD折叠得到△AED,AE交半圆于点F,连接DF.
(1)求证:DE是半圆的切线:
(2)连接0D,当OC=BC时,判断四边形ODFA的形状,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】威远人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,两种牛奶的总数不超过95件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)超过371元,请通过计算求出该商场购进甲、乙两种牛奶有哪几种方案?
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂第一车间有x人,第二车间比第一车间人数的 ![]() 少30人,从第二车间调出y人到第一车间,那么:
少30人,从第二车间调出y人到第一车间,那么:
(1)调动后,第一车间的人数为 人;第二车间的人数为 人.(用x,y的代数式表示);
(2)求调动后,第一车间的人数比第二车间的人数多几人(用x,y的代数式表示)?
(3)如果第一车间从第二车间调入的人数,是原来调入的10倍,则第一车间人数将达到360人,求实际调动后,(2)题中的具体人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com