
科目: 来源: 题型:
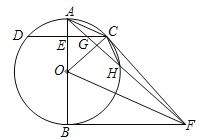
【题目】如图,已知AB是⊙O的直径,C是⊙O上任一点(不与A,B重合),AB⊥CD于E,BF为⊙O的切线,OF∥AC,连接AF,CF,AF与CD交于点G,与⊙O交于点H,连接CH.
(1)求证:CF是⊙O的切线;
(2)求证:EG=GC;
(3)若cos∠AOC=![]() ,⊙O的半径为9,求CH的长.
,⊙O的半径为9,求CH的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)计算:①13+(﹣22)﹣(﹣2)
②﹣4![]()
③(![]() ×(﹣48)
×(﹣48)
④﹣14﹣(![]() ﹣1)[﹣23+(﹣3)2]
﹣1)[﹣23+(﹣3)2]
(2)化简:①(3mn﹣2m2)+(﹣4m2﹣5mn)
②﹣(2a﹣3b)﹣2(﹣a+4b﹣1)
(3)先化简再求值:7x2y﹣2(2x2y﹣3xy2)-(4x2y﹣xy2),其中x=﹣2,y=1.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是由边长为1 的正方体搭成的立体图形,第(1)个图形由1个正方体搭成,第(2)个图形由4个正方体搭成,第(3)个图形由10个正方体搭成,以此类推,搭成第(6)个图形所需要的正方体个数是( )
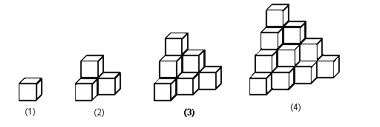
A.84个B.56个C.37个D.36个
查看答案和解析>>
科目: 来源: 题型:
【题目】请阅读下列材料:
问题:现有5个边长为1的正方形,排列形式如图①,请把它们分割后拼接成一个新的正方形,要求:画出分割线并在正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.小东同学的做法是:设新正方形的边长为x(x>0),依题意,割补前后图形的面积相等,有x2=5,解得![]() ,由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长,于是,画出如图②所示的分割线,拼出如图③所示的新正方形.
,由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长,于是,画出如图②所示的分割线,拼出如图③所示的新正方形.
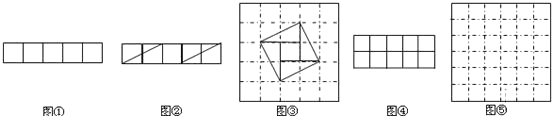
请你参考小东同学的做法,解决如下问题:
现有10个边长为1的正方形,排列形式如图④,请把它们分割后拼接成一个新的正方形,要求:在图④中画出分割线,并在图⑤的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.(说明:直接画出图形,不要求写分析过程.)
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙二人同时从学校出发,沿同一方向匀速行走,![]() 后,甲加快速度继续匀速行走(加速的时间忽略不计),乙始终匀速行走,两人都走了
后,甲加快速度继续匀速行走(加速的时间忽略不计),乙始终匀速行走,两人都走了![]() .两人在行走过程中得到如下表所示的信息:
.两人在行走过程中得到如下表所示的信息:
离开学校的时间 |
|
|
|
|
甲离学校的距离 |
|
|
|
|
乙离学校的距离 |
|
|
|
|
(1)根据题意,甲出发时的速度为_______![]() ,乙的速度为______
,乙的速度为______![]() ;
;
(2)求表中![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
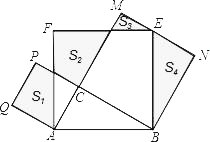
【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN,四块阴影部分的面积分别为S1、S2、S3、S4.则S1﹣S2+S3+S4等于_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本题满分10分)(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE,
填空:①∠AEB的度数为 ;
②线段AD、BE之间的数量关系是 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=900, 点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.

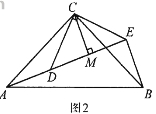
(3)解决问题如图3,在正方形ABCD中,CD=![]() .若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.
.若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.

查看答案和解析>>
科目: 来源: 题型:
【题目】某市居民使用自来水按月收费,标准如下:
①若每户月用水不超过![]() ,按
,按![]() 元/
元/![]() 收费;
收费;
②若超过![]() ,但不超过
,但不超过![]() ,则超过的部分按
,则超过的部分按![]() 元/
元/![]() 收费,未超过
收费,未超过![]() 部分按①标准收费;
部分按①标准收费;
③若超过![]() ,超过的部分按
,超过的部分按![]() 元/
元/![]() 收费,未超过
收费,未超过![]() 部分按②标准收费;
部分按②标准收费;
(1)若用水![]() ,应交水费______元;(用含
,应交水费______元;(用含![]() 的式子表示)
的式子表示)
(2)小明家上个月用水![]() ,交水费
,交水费![]() 元,求
元,求![]() 的值;
的值;
(3)在(2)的条件下,小明家七、八两个月共交水费![]() 元,七月份用水
元,七月份用水![]() 超过
超过![]() ,但不足
,但不足![]() ,八月份用水
,八月份用水![]() 超过
超过![]() ,当
,当![]() 均为整数时,求
均为整数时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com