
科目: 来源: 题型:
【题目】下表中有两种移动电话计费方式:

说明:月使用费固定收取,主叫不超限定时间不再收费,主叫超时部分加收超时费,被叫免费.
(1)若李明某月主叫通话时间为700分钟,则他按方式一计费需 元,按方式二计费需 元(用含![]() 的代数式表示);若他按方式一计费需60元,则主叫通话时间为 分钟;
的代数式表示);若他按方式一计费需60元,则主叫通话时间为 分钟;
(2)若方式二中主叫超时费![]() (元/分钟),是否存在某主叫通话时间
(元/分钟),是否存在某主叫通话时间![]() (分钟),按方式一和方式二的计费相等?若存在,请求出
(分钟),按方式一和方式二的计费相等?若存在,请求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)若主叫时间为750分钟时,两种方式的计费相等,直接写出![]() 的值为 ;请你通过计算分析后,直接给出当月主叫通话时间
的值为 ;请你通过计算分析后,直接给出当月主叫通话时间![]() (分钟)满足什么条件时,选择方式二省钱?
(分钟)满足什么条件时,选择方式二省钱?
查看答案和解析>>
科目: 来源: 题型:
【题目】蛋糕点厂生产大小两种月饼,下表是![]() 型、
型、![]() 型、
型、![]() 型三种月饼礼盒中装有大小两种月饼数量和需要消耗的面粉总重量的统计表.
型三种月饼礼盒中装有大小两种月饼数量和需要消耗的面粉总重量的统计表.

(1)直接写出制作1个大月饼要用 ![]() 面粉,制作1个小月饼要用
面粉,制作1个小月饼要用 ![]() 面粉;
面粉;
(2)直接写出![]() ,
,![]() ;
;
(3)经市场调研,该糕点厂要制作一批![]() 型月饼礼盒,现共有面粉63000
型月饼礼盒,现共有面粉63000![]() ,问制作大小两种月饼各用多少面粉,才能生产最多的
,问制作大小两种月饼各用多少面粉,才能生产最多的![]() 型月饼礼盒?
型月饼礼盒?
查看答案和解析>>
科目: 来源: 题型:
【题目】正方形ABCD的对角线AC,BD交于点O,作∠CBD的角平分线BE,分别交CD,OC于点E,F.
(1)依据题意,补全图形(用尺规作图,保留作图痕迹);
(2)求证:CE=CF;
(3)求证:DE=2OF.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的大小为α,面积记为S.

(1)请补全下表:
30° | 45° | 60° | 90° | 120° | 135° | 150° | |
S |
| 1 |
|
(2)填空:
由(1)可以发现正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把菱形的面积S记为S(α).例如:当α=30°时,![]() ;当α=135°时,
;当α=135°时,![]() .由上表可以得到
.由上表可以得到![]() ( ______°);
( ______°);![]() ( ______°),…,由此可以归纳出
( ______°),…,由此可以归纳出![]() .
.
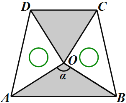
(3) 两块相同的等腰直角三角板按如图的方式放置,AD=![]() ,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,点M的坐标为(x1,y1),点N的坐标为(x2,y2),且x1≠x2,y1≠y2,以MN为边构造菱形,若该菱形的两条对角线分别平行于x轴,y轴,则称该菱形为边的“坐标菱形”,
(1)已知点A(2,0),B(0,2![]() ),则以AB为边的“坐标菱形”的面积为 ;
),则以AB为边的“坐标菱形”的面积为 ;
(2)若点C(1,2),点D在直线y=5上,以CD为边的“坐标菱形”为正方形,求直线CD解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数y=kx+b的图象与y轴交于点B(0,1),与反比例函数y=![]() 的图象交于点A(3,﹣2).
的图象交于点A(3,﹣2).
(1)求反比例函数的表达式和一次函数表达式;
(2)若点C是y轴上一点,且BC=BA,直接写出点C的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知点![]() .
.
(1)试按要求画图:
①连接![]() ,作射线
,作射线![]() ;
;
②画点![]() ,使
,使![]() 的值最小;
的值最小;
③画点![]() ,使点
,使点![]() 既在直线
既在直线![]() 上又在直线
上又在直线![]() 上.
上.
(2)填空:若点![]() 是线段
是线段![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上,
上,![]() ,
,![]() ,则
,则![]() 的长为 .
的长为 .
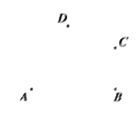
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,点D是抛物线![]()
![]() 的顶点,抛物线与x轴交于点A,B(点A在点B的左侧).
的顶点,抛物线与x轴交于点A,B(点A在点B的左侧).
(1)求点A,B的坐标;
(2)若M为对称轴与x轴交点,且DM=2AM,求抛物线表达式;
(3)当30°<∠ADM<45°时,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠A=30°,AB=6,点P是斜边AB上一点(点P不与点A,B重合),过点P作PQ⊥AB于P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y.
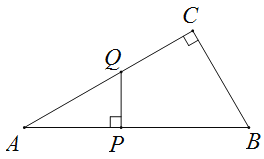
小明根据学习函数的经验,对函数y随自变量x的变换而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)通过取点、画图、测量、计算,得到了x与y的几组值,如下表:
x | …… | 0.8 | 1.0 | 1.4 | 2.0 | 3.0 | 4.0 | 4.5 | 4.8 | 5.0 | 5.5 | …… |
y | …… | 0.2 | 0.3 | 0.6 | 1.2 | 2.6 | 4.6 | 5.8 | 5.0 | m | 2.4 | …… |
经测量、计算,m的值是 (保留一位小数).
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合几何图形和函数图象直接写出,当QP=CQ时,x的值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com