
科目: 来源: 题型:
【题目】已知抛物线C:y=ax2-2ax+c经过点C(1,2),与x轴交于A(-1,0)、B两点
(1) 求抛物线C的解析式
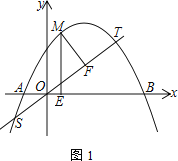
(2) 如图1,直线![]() 交抛物线C于S、T两点,M为抛物线C上A、T之间的动点,过M点作ME⊥x轴于点E,MF⊥ST于点F,求ME+MF的最大值
交抛物线C于S、T两点,M为抛物线C上A、T之间的动点,过M点作ME⊥x轴于点E,MF⊥ST于点F,求ME+MF的最大值
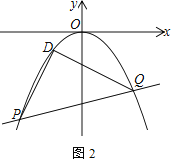
(3) 如图2,平移抛物线C的顶点到原点得抛物线C1,直线l:y=kx-2k-4交抛物线C1于P、Q两点,在抛物线C1上存在一个定点D,使∠PDQ=90°,求点D的坐标
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在白纸上画两条长度均为![]() 且夹角为
且夹角为![]() 的线段
的线段![]() 、
、![]() ,然后你把一支长度也为
,然后你把一支长度也为![]() 的铅笔
的铅笔![]() 放在线段
放在线段![]() 上,将这支铅笔以线段
上,将这支铅笔以线段![]() 上的一点
上的一点![]() 为旋转中心旋转顺时针旋转一周。
为旋转中心旋转顺时针旋转一周。
(1)若![]() 与
与![]() 重合,当旋转角为______时,这支铅笔与线段
重合,当旋转角为______时,这支铅笔与线段![]() 、
、![]() 围成的三角形是等腰三角形。
围成的三角形是等腰三角形。
(2)点![]() 从
从![]() 逐渐向
逐渐向![]() 移动,记
移动,记![]() :
:
①若![]() ,当旋转角为
,当旋转角为![]() 、______、______、______、
、______、______、______、![]() 、______时这支铅笔与线段
、______时这支铅笔与线段![]() 、
、![]() 共围成6个等腰三角形。
共围成6个等腰三角形。
②当这支铅笔与线段![]() 、
、![]() 正好围成5个等腰三角形时,求
正好围成5个等腰三角形时,求![]() 的取值范围。
的取值范围。
③当这支铅笔与线段![]() 、
、![]() 正好围成3个等腰三角形时,直接写出
正好围成3个等腰三角形时,直接写出![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目: 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目: 来源: 题型:
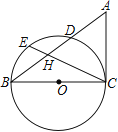
【题目】如图,BC是⊙O的直径,AB交⊙O于点D,E为弧BD的中点,CE交AB于点H,AC=AH
(1) 求证:AC与⊙O相切
(2) 若CH=3EH,求sin∠ABC的值
查看答案和解析>>
科目: 来源: 题型:
【题目】若抛物线上![]() ,它与
,它与![]() 轴交于
轴交于![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() ,
,![]() 是抛物线上
是抛物线上![]() 、
、![]() 之间的一点,
之间的一点,
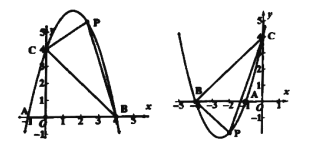
(1)当![]() 时,求抛物线的方程,并求出当
时,求抛物线的方程,并求出当![]() 面积最大时的
面积最大时的![]() 的横坐标。
的横坐标。
(2)当![]() 时,求抛物线的方程及
时,求抛物线的方程及![]() 的坐标,并求当
的坐标,并求当![]() 面积最大时
面积最大时![]() 的横坐标。
的横坐标。
(3)根据(1)、(2)推断![]() 的横坐标与
的横坐标与![]() 的横坐标有何关系?
的横坐标有何关系?
查看答案和解析>>
科目: 来源: 题型:
【题目】[问题背景]![]() 三边的长分别为
三边的长分别为![]() ,求这个三角形的面积.
,求这个三角形的面积.
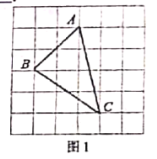
小辉同学在解这道题时,先建立一个正方形网格(每个小正方形的边长为![]() ),再在网格中作出格点
),再在网格中作出格点![]() (即
(即![]() 三个顶点都在小正方形的顶点处),如图1所示,这样不需要作
三个顶点都在小正方形的顶点处),如图1所示,这样不需要作![]() 的高,借用网格就能计算出
的高,借用网格就能计算出![]() 的面积为_ ;
的面积为_ ;
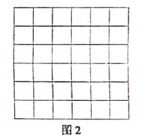
[思维拓展]我们把上述求![]() 面积的方法叫做构图法,若
面积的方法叫做构图法,若![]() 三边的长分别为
三边的长分别为![]() ,请利用图2的正方形网格(每个小正方形的边长为
,请利用图2的正方形网格(每个小正方形的边长为![]() )画出相应的
)画出相应的![]() ,并求出它的面积:
,并求出它的面积:
[探索创新]若![]() 三边的长分别为
三边的长分别为![]() (其中
(其中![]() 且
且![]() ),请利用构图法求出这个三角形的面积(画出图形并计算面积).
),请利用构图法求出这个三角形的面积(画出图形并计算面积).
查看答案和解析>>
科目: 来源: 题型:
【题目】作图题:在图(1)(2)所示抛物线中,抛物线与![]() 轴交于
轴交于![]() 、
、![]() ,与
,与![]() 轴交于
轴交于![]() ,点
,点![]() 是抛物线的顶点,过
是抛物线的顶点,过![]() 平行于
平行于![]() 轴的直线是它的对称轴,点
轴的直线是它的对称轴,点![]() 在对称轴上运动。仅用无刻度的直尺画线的方法,按要求完成下列作图:
在对称轴上运动。仅用无刻度的直尺画线的方法,按要求完成下列作图:

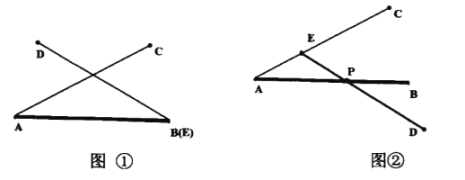
(1)在图①中作出点![]() ,使线段
,使线段![]() 最小;
最小;
(2)在图②中作出点![]() ,使线段
,使线段![]() 最大.
最大.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两辆汽车同时从相距![]() 千米的
千米的![]() 两地沿同条公路相向而行(甲由
两地沿同条公路相向而行(甲由![]() 到
到![]() ,乙由
,乙由![]() 到
到![]() ).如图,
).如图,![]() 分别表示两辆汽车与
分别表示两辆汽车与![]() 地之间的距离
地之间的距离![]() 与行驶时间
与行驶时间![]() 之间的关系.
之间的关系.
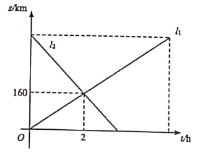
![]() 分别求
分别求![]() 对应的函数表达式;
对应的函数表达式;
![]() 甲车到达
甲车到达![]() 地比乙车到达
地比乙车到达![]() 地多用_ 小时;
地多用_ 小时;
![]() 出发多少小时后,两车相距
出发多少小时后,两车相距![]() 千米?
千米?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知两条线段长分别是一元二次方程![]() 的两根,
的两根,
(1)解方程求两条线段的长。
(2)若把较长的线段剪成两段,使其与另一段围成等腰三角形,求等腰三角形的面积。
(3)若把较长的线段剪成两段,使其与另一段围成直角三角形,求直角三角形的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com