
科目: 来源: 题型:
【题目】如图,一楼房AB后有一假山,其坡比i=1∶![]() ,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=25 m,与亭子距离CE=20 m.小丽从楼房顶测得点E的俯角为45°,求楼房AB的高.
,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=25 m,与亭子距离CE=20 m.小丽从楼房顶测得点E的俯角为45°,求楼房AB的高.

查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面一段文字:
问题:![]() 能化为分数形式吗?
能化为分数形式吗?
探求:步骤①设![]() ,步骤②
,步骤②![]() ,
,
步骤③![]() ,则
,则![]() ,
,
步骤④![]() ,解得:
,解得:![]() .
.
根据你对这段文字的理解,回答下列问题:
(1)步骤①到步骤②的依据是什么;
(2)仿照上述探求过程,请你尝试把![]() 化为分数形式:
化为分数形式:
(3)请你将![]() 化为分数形式,并说明理由.
化为分数形式,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在半径为r的⊙O中,直径AB与弦CD相交于点P,CE⊥DA交DA的延长线于点E,连结AC.
(1)若![]() 的长为
的长为![]() πr,求∠ACD的度数;
πr,求∠ACD的度数;
(2)若![]() ,tan∠DAB=3,CE-AE=3,求r的值.
,tan∠DAB=3,CE-AE=3,求r的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD=2米),背水坡DE的坡度i=1:1(即DB:EB=1:1),如图所示,已知AE=4米,∠EAC=130°,求水坝原来的高度BC.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)
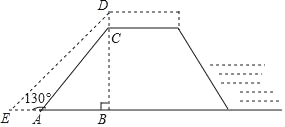
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.
其中说法正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:![]() .
.
(1)求新坡面的坡角∠CAB的度数;
(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除?请说明理由.
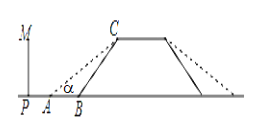
查看答案和解析>>
科目: 来源: 题型:
【题目】一次函数y=kx﹣1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为( )
A. (﹣5,3) B. (1,﹣3) C. (2,2) D. (5,﹣1)
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)阅读思考:
小迪在学习过程中,发现“数轴上两点间的距离”可以用“表示这两点数的差”来表示,探索过程如下:
如图1所示,线段AB,BC,CD的长度可表示为:AB=3=4﹣1,BC=5=4﹣(﹣1),CD=3=(﹣1)﹣(﹣4),于是他归纳出这样的结论:如果点A表示的数为a,点B表示的数为b,当b>a时,AB=b﹣a(较大数﹣较小数).

(2)尝试应用:
①如图2所示,计算:OE= ,EF= ;
②把一条数轴在数m处对折,使表示﹣19和2019两数的点恰好互相重合,则m= ;

(3)问题解决:
①如图3所示,点P表示数x,点M表示数﹣2,点N表示数2x+8,且MN=4PM,求出点P和点N分别表示的数;
②在上述①的条件下,是否存在点Q,使PQ+QN=3QM?若存在,请直接写出点Q所表示的数;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形![]() 中;点
中;点![]() 为坐标原点,点
为坐标原点,点![]() ,点
,点![]() 、
、![]() 在坐标轴上,点
在坐标轴上,点![]() 在
在![]() 边上,直线
边上,直线![]() 交
交![]() 轴于点
轴于点![]() .对于坐标平面内的直线,先将该直线向右平移
.对于坐标平面内的直线,先将该直线向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位长度,这种直线运动称为直线的斜平移.现将直线
个单位长度,这种直线运动称为直线的斜平移.现将直线![]() 经过
经过![]() 次斜平移,得到直线
次斜平移,得到直线![]() .
.


(备用图)
(1)求直线![]() 与两坐标轴围成的面积;
与两坐标轴围成的面积;
(2)求直线![]() 与
与![]() 的交点坐标;
的交点坐标;
(3)在第一象限内,在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 是等腰直角三角形?若存在,请直接写出点
是等腰直角三角形?若存在,请直接写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com