
科目: 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④![]() <a<
<a<![]() ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )

A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
查看答案和解析>>
科目: 来源: 题型:
【题目】老师在讲“实数”时画了一个图(如图),即“以数轴的单位长度为边作一个正方形,然后以原点为圆心,正方形的对角线长为半径画弧交数轴于点A.

(1)A点表示的数是多少?在数轴上,A点与表示一1.42的点有什么位置关系;
(2)你认为老师作这样的图是为了说明什么?
(3)请类比上面的作法在数轴上画出表示-![]() 的点B.(请保留作图痕迹)
的点B.(请保留作图痕迹)
查看答案和解析>>
科目: 来源: 题型:
【题目】对于抛物线y=-x2+2x+3,有下列四个结论:①它的对称轴为x=1;
②它的顶点坐标为(1,4);
③它与y轴的交点坐标为(0,3),与x轴的交点坐标为(-1,0)和(3,0);
④当x>0时,y随x的增大而减小.
其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】完成下面的证明,如图点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA.求证:∠FDE=∠A.
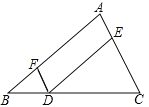
证明:∵DE∥AB,
∴∠FDE=∠ ( )
∵DF∥CA,
∴∠A=∠ ( )
∴∠FDE=∠A( )
查看答案和解析>>
科目: 来源: 题型:
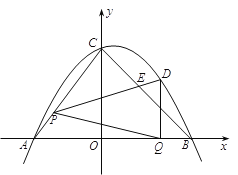
【题目】如图,在平面直角坐标系![]() 中,已知A(-3,0),B(4,0),C(0,4). 二次函数的图像经过A、B、C三点.点P沿AC由点A处向点C运动,同时,点Q沿BO由点B处向点O运动,运动速度均为每秒1个单位长度.当一个点停止运动时,另一个点也随之停止运动.连接PQ,过点Q作QD⊥x轴,与二次函数的图像交于点D,连接PD,PD与BC交于点E. 设点P的运动时间为t秒(t>0).
中,已知A(-3,0),B(4,0),C(0,4). 二次函数的图像经过A、B、C三点.点P沿AC由点A处向点C运动,同时,点Q沿BO由点B处向点O运动,运动速度均为每秒1个单位长度.当一个点停止运动时,另一个点也随之停止运动.连接PQ,过点Q作QD⊥x轴,与二次函数的图像交于点D,连接PD,PD与BC交于点E. 设点P的运动时间为t秒(t>0).
⑴ 求二次函数的表达式;
⑵ 在点P、Q运动的过程中,当∠PQA+∠PDQ=90°时,求t的值;
⑶ 连接PB、BD、CD,试探究在点P,Q运动的过程中,是否存在某一时刻,使得四边形PBDC是平行四边形?若存在,请求出此时t的值与点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 所在平面内一点,过点
所在平面内一点,过点![]() 分别作
分别作![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
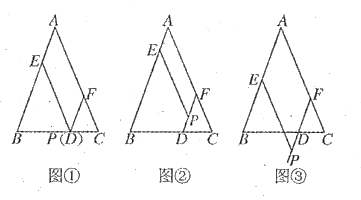
若点![]() 在
在![]() 上(如图①),此时
上(如图①),此时![]() ,可得结论:
,可得结论:![]() .
.
请应用上述信息解决下列问题:
当点![]() 分别在
分别在![]() 内(如图②),
内(如图②),![]() 外(如图③)时,上述结论是否成立?若成立,请给予证明;若不成立,
外(如图③)时,上述结论是否成立?若成立,请给予证明;若不成立,![]() ,
,![]() ,
,![]() ,与
,与![]() 之间又有怎样的数量关系,请写出你的猜想,不需要证明.
之间又有怎样的数量关系,请写出你的猜想,不需要证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.

(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间有何关系?说明理由.
(3)若点P在Rt△ABC斜边BA的延长线上运动(CE<CD),则∠α、∠1、∠2之间有何关系?猜想并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,点P是边AD上的动点(点P不与点A、点D重合),点Q是边CD上一点,连接PB、PQ,且∠PBC=∠BPQ.
⑴ 若tan∠PBC=4,求AP的长;
⑵ 是否存在点P,使得点Q恰好是边CD的中点?若存在,求出AP的长;若不存在,请说明理由.⑶ 连接BQ,在△PBQ中是否存在度数不变的角?若存在,指出这个角,并求出它的度数;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】⑴ 阅读理解
问题1:已知a、b、c、d为正数,![]() ,ac=bd,试说明a=d,b=c.
,ac=bd,试说明a=d,b=c.
我们通过构造几何模型解决代数问题. 注意到条件![]() ,如果把a、b、c、d分别看作为两个直角三角形的直角边,那么可构造图1所示的几何模型.
,如果把a、b、c、d分别看作为两个直角三角形的直角边,那么可构造图1所示的几何模型.
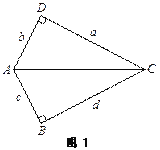
∵ac=bd,
∴AB·CD=BC·AD
∴![]()
请你按照以上思路继续完成说明.
⑵ 深入探究
问题2:若a>0,b>0,试比较![]() 和
和![]() 的大小.
的大小.
为此我们构造图2所示的几何模型,其中AB为直径, O为圆心,点C在半圆上,CD⊥AB 于D,AD=a,BD=b.
请你利用图2所示的几何模型解决提出的问题2.
⑶ 拓展运用
对于函数y=x+![]() ,求当x>0时,求y的取值范围.
,求当x>0时,求y的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:
某些代数恒等式可用一些卡片拼成的图形的面积来解释.例如,图①可以解释![]() ,因此,我们可以利用这种方法对某些多项式进行因式分解.
,因此,我们可以利用这种方法对某些多项式进行因式分解.
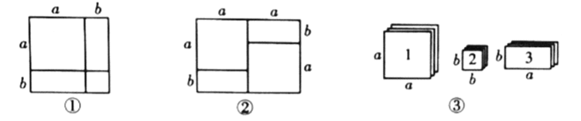
根据阅读材料回答下列问题:
(1)如图②所表示的因式分解的恒等式是________________________.
(2)现有足够多的正方形和长方形卡片(如图③),试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的长方形(每两张卡片之间既不重叠,也无空隙),使该长方形的面积为![]() ,并利用你画的长方形的面积对
,并利用你画的长方形的面积对![]() 进行因式分解.
进行因式分解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com