
科目: 来源: 题型:
【题目】日照间距系数反映了房屋日照情况.如图①,当前后房屋都朝向正南时,日照间距系数=L:(H﹣H1),其中L为楼间水平距离,H为南侧楼房高度,H1为北侧楼房底层窗台至地面高度.
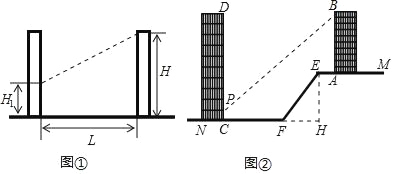
如图②,山坡EF朝北,EF长为15m,坡度为i=1:0.75,山坡顶部平地EM上有一高为22.5m的楼房AB,底部A到E点的距离为4m.
(1)求山坡EF的水平宽度FH;
(2)欲在AB楼正北侧山脚的平地FN上建一楼房CD,已知该楼底层窗台P处至地面C处的高度为0.9m,要使该楼的日照间距系数不低于1.25,底部C距F处至少多远?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(m,2)在直线![]() :y=2x上,过点A的直线
:y=2x上,过点A的直线![]() 与x轴交于点B(4,0).
与x轴交于点B(4,0).
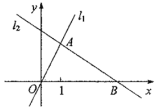
(1)求直线![]() 的解析式;
的解析式;
(2)己知点P.的坐标为(n,0),过点P垂直x轴的直线与![]() ,
,![]() 分别交于点C,D,当点C位于点D上方时,求n的取值范围.
分别交于点C,D,当点C位于点D上方时,求n的取值范围.
查看答案和解析>>
科目: 来源: 题型:
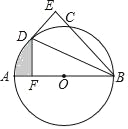
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)试判断DE与⊙O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3![]() ,DF=3,求图中阴影部分的面积.
,DF=3,求图中阴影部分的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】乔亚萍和张红武做游戏,乔亚萍说:“你在心中想好一个两位数,对这个两位数进行如下的运算:①这个两位数的十位数字和个位数字相加,将所得的和乘以11;②用原两位数的十位数字减去个位数字,将所得的差乘以9;③用①中所得的结果减去②中所得的结果,所得的差加上16,得到最终的结果,把这个结果告诉我,我就能猜出你心中想的数了.”张红武算的结果为50,请帮乔亚萍算出张红武心中想的数为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】某软件科技公司20人负责研发与维护游戏、网购、视频和送餐共4款软件.投入市场后,游戏软件的利润占这4款软件总利润的40%.如图是这4款软件研发与维护人数的扇形统计图和利润的条形统计图.
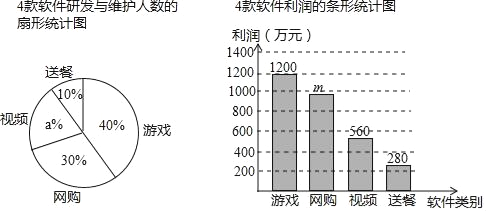
根据以上信息,网答下列问题
(1)直接写出图中a,m的值;
(2)分别求网购与视频软件的人均利润;
(3)在总人数和各款软件人均利润都保持不变的情况下,能否只调整网购与视频软件的研发与维护人数,使总利润增加60万元?如果能,写出调整方案;如果不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
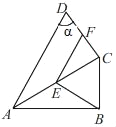
【题目】如图,四边形ABCD中,AC平分∠BAD,∠ACD=∠ABC=90°,E、F分别为AC、CD的中点,∠D=α,则∠BEF的度数为_____(用含α的式子表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】对于数轴上的A、B、C三点,给出如下定义:若其中一个点与其它两个点的距离恰好满足2倍的数量关系,则称该点是其它两个点的“至善点”.例如:若数轴上点A、B、C所表示的数分别为1、3、4,则点B是点A、C的“至善点”.
(1)若点A表示数﹣2,点B表示数2,下列各数![]() 、0、1、6所对应的点分别为C1、C2、C3、C4,其中是点A、B的“至善点”的有 (填代号);
、0、1、6所对应的点分别为C1、C2、C3、C4,其中是点A、B的“至善点”的有 (填代号);
(2)已知点A表示数﹣1,点B表示数3,点M为数轴上一个动点:
①若点M在点A的左侧,且点M是点A、B的“至善点”,求此时点M表示的数m;
②若点M在点B的右侧,点M、A、B中,有一个点恰好是其它两个点的“至善点”,求出此时点M表示的数m.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:平行四边形ABCD,求作菱形AECF,使点E、点F分别在BC、AD边上
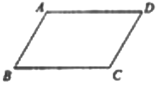
下面是小明设计的尺规作图过程.
作法:如图
① 连接AC;
② 分别以A、C为圆心,大于![]() AC的长为半径作弧,两弧交于M、N两点;
AC的长为半径作弧,两弧交于M、N两点;
③ 连接MN,分别与BC、AD、AC交于E、F、O三点;
④ 连接AE、CF
四边形AECF即为所求
根据小明设计的尺规作图过程
(1)使用直尺和圆规,补全图形:(保留作图痕迹)
(2)完成下面的证明
证明∵AM= ,AN= ,
∴MN是AC的垂直平分线。
( )(填推理的依据)
∴EF⊥AC,OA=OC,
∴平行四边形ABCD
∴AD∥BC
∴∠FAO=∠ECO
在△FAO和△ECO中

∴△FAO≌△ECO
∴OE=OF
又∵OA=OC
∴四边形AECF是平行四边形
( )(填推理依据)
∵EF⊥AC
∴四边形AECF是菱形
( )(填推理依据)
查看答案和解析>>
科目: 来源: 题型:
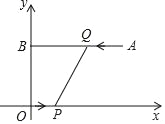
【题目】如图,平面直角坐标系xOy中,点A的坐标为(9,6),AB⊥y轴,垂足为B,点P从原点O出发向x轴正方向运动,同时,点Q从点A出发向点B运动,当点Q到达点B时,点P、Q同时停止运动,若点P与点Q的速度之比为1:2,则下列说法正确的是( )
A. 线段PQ始终经过点(2,3)
B. 线段PQ始终经过点(3,2)
C. 线段PQ始终经过点(2,2)
D. 线段PQ不可能始终经过某一定点
查看答案和解析>>
科目: 来源: 题型:
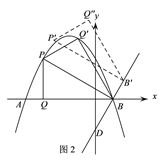
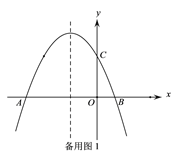
【题目】如图,抛物线y=-![]() x2-
x2-![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴于点C,已知点D(0,-
与x轴交于A、B两点(点A在点B的左侧),与y轴于点C,已知点D(0,-![]() ).
).
(1)求直线AC的解析式;
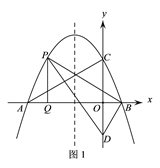
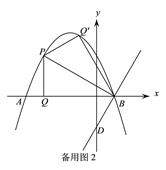
(2)如图1,P为直线AC上方抛物线上的一动点,当△PBD的面积最大时,过P作PQ⊥x轴于点Q,M为抛物线对称轴上的一动点,过M作y轴的垂线,垂足为点N,连接PM、NQ,求PM+MN+NQ的最小值;
(3)在(2)问的条件下,将得到的△PBQ沿PB翻折得到△PBQ′,将△PBQ′沿直线BD平移,记平移中的△PBQ′为△P′B′Q″,在平移过程中,设直线P′B′与x轴交于点E,则是否存在这样的点E,使得△B′EQ″为等腰三角形?若存在,求此时OE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com