
科目: 来源: 题型:
【题目】西安市管理部门对“十一”国庆放假期间七天本市某景区客流变化量进行了不完全统计,数据如下(用正数表示客流量比前一天增加,用负数表示客流量比前一天下降):
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
变化(万人) |
|
|
|
|
|
|
|
请通过计算解决以下问题:
(1)请判断这7天中,哪一天人数最多?哪一天人数最少?
(2)与10月3日相比,10月5日的客流量是上升了还是下降了?
(3)如图9月30日的客流量为1.5万人,据统计平均每人每天消费200元,请问该景区在“十一”七天国庆假期的总收入为多少万元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )

A. 4B. 3C. 2D. 1
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD的边长为2,.过B作BE//AC.
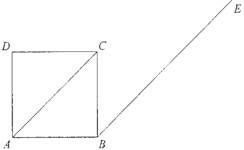
(1)求BE与AC之间的距离;
(2)F为BE上一点,连接AF,过C作CG//AF交BE于G.若∠FAB=15°,
①依题意补全图形;
②求证:四边形AFGC是菱形.
查看答案和解析>>
科目: 来源: 题型:
【题目】用一样长的小木棒按下图中的方式搭图形.
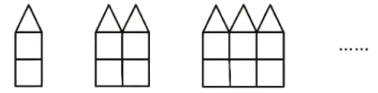
(1)按图示规律填空:
图形标号 | ① | ② | ③ | … |
小木棒的根数 | 9 | … |
(2)按照这种规律搭下去,搭第![]() 个图形需要________根小木棒;
个图形需要________根小木棒;
(3)请求出搭第100个图形需要的小木棒的根数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD中,AB=2,动点P从点B出发,以每秒1个单位的速度在正方形的边上沿BC-CD-DA运动,设运动时间为t,△PAB面积为S.

(1)求S关于t的函数解析式,并写出自变量t的取值范围;
(2)画出相应函数图象;
(3)当S=![]() 时,t的值为多少.
时,t的值为多少.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,以![]() 为圆心,半径为
为圆心,半径为![]() 的圆与
的圆与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 、
、![]() 两点,点
两点,点![]() 为⊙
为⊙![]() 上一动点,
上一动点,![]() 于
于![]() ,则弦
,则弦![]() 的长度为__________,当点
的长度为__________,当点![]() 在⊙
在⊙![]() 上运动的过程中,线段
上运动的过程中,线段![]() 的长度的最小值为__________.
的长度的最小值为__________.
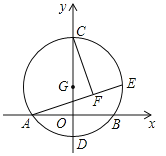
查看答案和解析>>
科目: 来源: 题型:
【题目】平面直角坐标系xOy中,横坐标为a的点A在反比例函数y1═![]() (x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(1)设a=2,点B(4,2)在函数y1、y2的图象上.
①分别求函数y1、y2的表达式;
②直接写出使y1>y2>0成立的x的范围;
(2)如图①,设函数y1、y2的图象相交于点B,点B的横坐标为3a,△AA'B的面积为16,求k的值;
(3)设m=![]() ,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
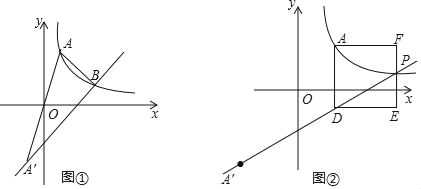
查看答案和解析>>
科目: 来源: 题型:
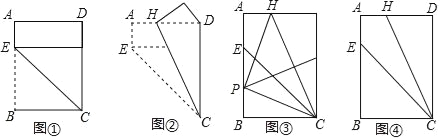
【题目】对给定的一张矩形纸片ABCD进行如下操作:先沿CE折叠,使点B落在CD边上(如图①),再沿CH折叠,这时发现点E恰好与点D重合(如图②)
(1)根据以上操作和发现,求![]() 的值;
的值;
(2)将该矩形纸片展开.
①如图③,折叠该矩形纸片,使点C与点H重合,折痕与AB相交于点P,再将该矩形纸片展开.求证:∠HPC=90°;
②不借助工具,利用图④探索一种新的折叠方法,找出与图③中位置相同的P点,要求只有一条折痕,且点P在折痕上,请简要说明折叠方法.(不需说明理由)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AC是□ ABCD的对角线,延长BA至点E,使AE=AB,连接DE.
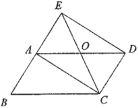
(1)求证:四边形ACDE是平行四边形;
(2)连接EC交AD于点O,若∠EOD=2∠B,求证:四边形ACDE是矩形.
查看答案和解析>>
科目: 来源: 题型:
【题目】平面直角坐标系xOy中,二次函数y=x2﹣2mx+m2+2m+2的图象与x轴有两个交点.
(1)当m=﹣2时,求二次函数的图象与x轴交点的坐标;
(2)过点P(0,m﹣1)作直线1⊥y轴,二次函数图象的顶点A在直线l与x轴之间(不包含点A在直线l上),求m的范围;
(3)在(2)的条件下,设二次函数图象的对称轴与直线l相交于点B,求△ABO的面积最大时m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com