
科目: 来源: 题型:
【题目】出租车司机小张某天上午营运全是在东西走向的政府大道上进行的,如果规定向东为正,向西为负,他这天上午的行程是(单位:千米):+15,-3,+16,-11,+10,-12,+4,-15,+16,-18.
(1)将最后一名乘客送达目的地时,小张距上午出发点的距离是多少千米?在出发点的什么方向?
(2)若汽车耗油量为0.6升/千米,出车时,邮箱有油72.2升,若小张将最后一名乘客送达目的地,再返回出发地,问小张今天上午是否需要加油?若要加油至少需要加多少才能返回出发地?若不用加油,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( )

A. AE=EF B. AB=2DE
C. △ADF和△ADE的面积相等 D. △ADE和△FDE的面积相等
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在△ABC中,∠BAC的平分线AD交BC于点D,DE垂直平分AC,垂足为点E.
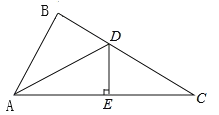
(1)证明∠BAD=∠C;
(2)∠BAD=29°,求∠B的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点.网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1 (要求A与A1,B与B1,C与C1相对应);
(2)求△ABC的面积;
(3)在直线l上找一点P,使得△PAC的周长最小.

查看答案和解析>>
科目: 来源: 题型:
【题目】(探索发现)有绝对值的定义可得,数轴上表示数![]() 的点到原点的距离为
的点到原点的距离为![]() .小丽进一步探究发现,在数轴上,表示3和5的两点之间的距离为
.小丽进一步探究发现,在数轴上,表示3和5的两点之间的距离为![]() ;表示
;表示![]() 和5的两点之间的距离为
和5的两点之间的距离为![]() ;表示
;表示![]() 和
和![]() 的两点之间的距离为
的两点之间的距离为![]() .
.
(概括总结)根据以上过程可以得出:数轴上,表示数![]() 和数
和数![]() 的两点之间的距离为
的两点之间的距离为![]() .
.
(问题解决)
(1)若![]() ,则
,则![]() ________;
________;
(2)若![]() ,则
,则![]() ________;
________;
(3)若![]() ,则
,则![]() ________.
________.
查看答案和解析>>
科目: 来源: 题型:
【题目】(![]() )如图
)如图![]() ,
,![]() 中,
中,![]() ,
,![]() 是
是![]() 上任意一点,以点
上任意一点,以点![]() 为中心,取旋转角等于
为中心,取旋转角等于![]() ,把
,把![]() 逆时针旋转,画出旋转后的图形.
逆时针旋转,画出旋转后的图形.
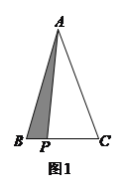
(![]() )如图
)如图![]() ,等边
,等边![]() 中,
中,![]() 为
为![]() 边上一点,
边上一点,![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
求证:![]() .
.
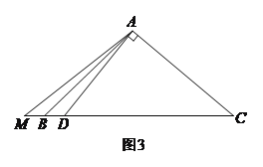
(![]() )已知:如图
)已知:如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() ,已知
,已知![]() ,
,![]() .写出求线段
.写出求线段![]() 长的具体思路(即添加辅助线的方法,推导的具体步骤详写,其它的写出关键步骤或结果即可),并给出最后结果.
长的具体思路(即添加辅助线的方法,推导的具体步骤详写,其它的写出关键步骤或结果即可),并给出最后结果.

查看答案和解析>>
科目: 来源: 题型:
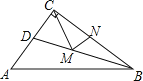
【题目】如图,△ABC中,∠ACB=90°,AC =3,BC =4,AB=5,BD平分∠ABC,如果M、N分别为BD、BC上的动点,那么CM+MN的最小值是____.
查看答案和解析>>
科目: 来源: 题型:
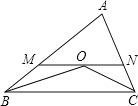
【题目】如图,△ABC的两条角平分线相交于O,过O的直线MN∥BC交AB于M交AC于N,若BC=8cm,△AMN的周长是12cm,则△ABC的周长等于_____cm.
查看答案和解析>>
科目: 来源: 题型:
【题目】在一块长![]() ,宽为
,宽为![]() 的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,下面分别是小华与小芳的设计方案.
的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,下面分别是小华与小芳的设计方案.
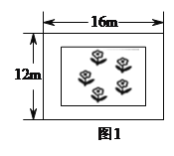
(![]() )小芳说,‘我的设计方案如图所示,平行于荒地的四边建造矩形的花园,花园四周小路的宽度均相同’,你能帮小芳算出小路的宽度吗?请利用方程的方法计算出小路的宽度.
)小芳说,‘我的设计方案如图所示,平行于荒地的四边建造矩形的花园,花园四周小路的宽度均相同’,你能帮小芳算出小路的宽度吗?请利用方程的方法计算出小路的宽度.
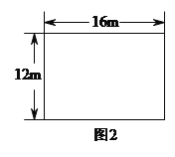
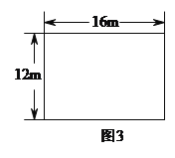
(![]() )小华说,‘我的设计方案是建造一个中心对称的四边形的花园,并且这个四边形的四个顶点分别在矩形荒地的四条边上’,请你按小华的思路,分别设计符合条件的一个菱形和一个矩形,在图
)小华说,‘我的设计方案是建造一个中心对称的四边形的花园,并且这个四边形的四个顶点分别在矩形荒地的四条边上’,请你按小华的思路,分别设计符合条件的一个菱形和一个矩形,在图![]() 和图
和图![]() 中画出相应的草图,说明所画图形的特征,并简述所画图形符合要求的理由.
中画出相应的草图,说明所画图形的特征,并简述所画图形符合要求的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com