
科目: 来源: 题型:
【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,O是直线AB上的一点,∠AOC=45°,OE是∠BOC内部的一条射线,且OF平分∠AOE.
(1)如图1,若∠COF=35°,求∠EOB的度数;
(2)如图2,若∠EOB=40°,求∠COF的度数;
(3)如图3,∠COF与∠EOB有怎样的数量关系?请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC外,若∠2=18°,则∠1的度数为( )
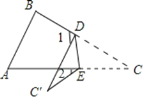
A. 50°B. 98°C. 75°D. 80°
查看答案和解析>>
科目: 来源: 题型:
【题目】整式计算题
(1)先化简,再求值:(3x2﹣xy+y)﹣2(5xy﹣4x2+2y),其中x=2,y=1.
(2)已知小明的年龄是m岁,小红的年龄比小明的年龄的2倍少4岁,小华的年龄比小红的年龄的![]() 还多1岁,求这三名同学的年龄的和.
还多1岁,求这三名同学的年龄的和.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,这是网上盛传的一个关于数学的诡辩问题截图,表1是它的示意表.我们一起来解答“为什么多出了![]() 元”.
元”.

表1
花去 | 剩余 | |
买牛肉 |
|
|
买猪脚 |
|
|
买蔬菜 |
|
|
买调料 |
|
|
总计 |
|
|
(1)为了解释“剩余金额总计”与“我手里有![]() 元”无关,按要求填写表2中的空格.
元”无关,按要求填写表2中的空格.
表2
花去 | 剩余 | |
买牛肉 |
|
|
买猪脚 |
|
|
买蔬菜 | 元 | 元 |
买调料 | 元 |
|
总计 |
|
|
表3
花去 | 剩余 | |
买物品1 |
|
|
买物品2 |
|
|
买物品3 |
|
|
买物品4 |
|
|
总计 |
|
|
(2)如表3中,直接写出以下各代数式的值:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
(3)如表3中,![]() 都是正整数,则
都是正整数,则![]() 的最大值等于 ;最小值等于 .由此可以知道“为什么多出了
的最大值等于 ;最小值等于 .由此可以知道“为什么多出了![]() 元”只是一个诡辩而已.
元”只是一个诡辩而已.
(4)我们将“花去”记为“![]() ”,“剩余”记为“
”,“剩余”记为“![]() ”,请在表4中将表1数据重新成号.
”,请在表4中将表1数据重新成号.
花去 | 剩余 | |
买牛肉 | 元 | 元 |
买猪脚 | 元 | 元 |
买蔬菜 | 元 | 元 |
买调料 | 元 | 元 |
总计 | 元 |
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的个数是( )
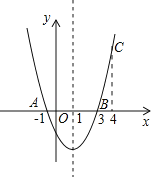
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】已知: ![]() ,
,![]() .
.
(1)当x=1和-1时,分别求P,Q的值;
(2)当x=19时,P的值为a, Q的值为b,当x=-19时,分别求P, Q的值(用含a,b的代数式表示);
(3)当x=m时,P, Q的值分别为c, d; 当x=-m时,P, Q的值分别为e, f,则在c,d, e, f四个有理数中,以下判断正确的是 (只要填序号即可).
①有两个相等的正数;②有两个互为相反数;③至多有两个正数;④至少有两个正数;⑤至多有一个负数;⑥至少有一个负数.
查看答案和解析>>
科目: 来源: 题型:
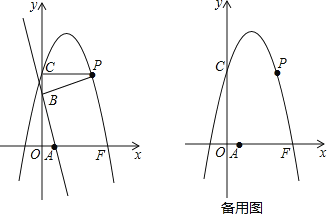
【题目】如图,直线y=﹣3x+3与x轴、y轴分别交于A,B两点,抛物线y=﹣x2+bx+c与直线y=c分别交y轴的正半轴于点C和第一象限的点P,连接PB,得△PCB≌△BOA(O为坐标原点).若抛物线与x轴正半轴交点为点F,设M是点C,F间抛物线上的一点(包括端点),其横坐标为m.
(1)直接写出点P的坐标和抛物线的解析式;
(2)当m为何值时,△MAB面积S取得最小值和最大值?请说明理由;
(3)求满足∠MPO=∠POA的点M的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】先阅读材料,再结合要求回答问题.
【问题情景】
如图①:在四边形ABCD中,AB=AD,∠B=∠ADC=90°.E,F分别是BC,CD上的点,且线段BE,EF,FD满足BE+FD=EF.试探究图中∠EAF与∠BAD之间的数量关系.

【初步思考】
小王同学探究此问题的方法是:延长FD到G,使DG=BE,连结AG.
先证明△ABE≌△ADG,再证明△AEF≌△AGF,
可得出∠EAF与∠BAD之间的数量关系是 .
【探索延伸】
若将问题情景中条件“∠B=∠ADC=90°”改为“∠B+∠D=180°”(如图②),其余条件不变,请判断上述数量关系是否仍然成立,若成立,请证明;若不成立,请说明理由.
【实际应用】
如图③,在某次军事演习中,舰艇甲在指挥中心(O)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处且相距210海里.试求此时两舰艇的位置与指挥中心(O处)形成的夹角∠EOF的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com