
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,B点坐标为(﹣2,0),A点坐标为(a,b),且b≠0.
(1)若b>0,且∠ABO:∠BAO:∠AOB=10:5:21,在AB上取一点C,使得y轴平分∠COA.在x轴上取点D,使得CD平分∠BCO,过C作CD的垂线CE,交x轴于E.
①依题意补全图形;
②求∠CEO的度数;
(2)若b是定值,过O作直线AB的垂线OH,垂足为H,则OH的最大值是 .(直接写出答案)

查看答案和解析>>
科目: 来源: 题型:
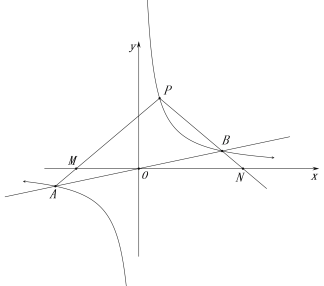
【题目】如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点A,B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
的图象交于点A,B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
(1)求k的值;
(2)设直线PA,PB与x轴分别交于点M,N,求证:△PMN是等腰三角形;
(3)设点Q是反比例函数图象上位于P,B之间的动点(与点P,B不重合),连接AQ,BQ,比较∠PAQ与∠PBQ的大小,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,
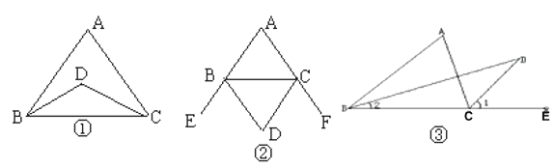
(1)如图①,BD、CD是∠ABC和∠ACB的角平分线且相交于点D,若∠A =70°,试求∠BDC的度数,并说明理由。
(2)如图②,BD、CD分别是△ABC外角∠EBC、∠FCB的平分线且相交于点D,若∠A =x°,试用x表示∠BDC的度数,并说明理由。
(3)如图③,BD、CD分别是∠ABC和△ACB外角∠ACE的平分线且相交于点D,试找出∠A与∠BDC之间的数量关系,并说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,线段AB、CD相交于点O,连结AD、CB,我们把这个图形称为“8字型”根据三角形内角和容易得到:∠A+∠D=∠C+∠B.


(1)用“8字型”
如图2,∠A+∠B+∠C+∠D+∠E+∠F=___________;
(2)造“8字型”
如图3,∠A+∠B+∠C+∠D+∠E+∠F+∠G=_____________;
(3)发现“8字型”
如图4,BE、CD相交于点A,CF为∠BCD的平分
线,EF为∠BED的平分线.
①图中共有________个“8字型”;
②若∠B:∠D:∠F=4:6:x,求x的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了了解2019年北京市乘坐地铁的每个人的月均花费情况,相关部门随机调查了1000人乘坐地铁的月均花费(单位:元),绘制了如下频数分布直方图,根据图中信息,下面三个推断中,合理的是( )
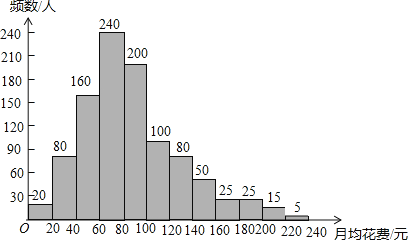
①小明乘坐地铁的月均花费是75元,那么在所调查的1000人中一定有超过一半的人月均花费超过小明;
②估计平均每人乘坐地铁的月均花费的不低于60元;
③如果规定消费达到一定数额可以享受折扣优惠,并且享受折扣优惠的人数控制在20%左右,那么乘坐地铁的月均花费达到120元的人可享受折扣.
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目: 来源: 题型:
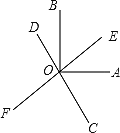
【题目】如图,直线EF、CD相交于点O,OA⊥OB,OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=30°,请直接写出∠BOD的度数;
(3)观察(1)(2)的结果,猜想∠AOE和∠BOD的数量关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=3m.小亮在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=2m,点A到地面的距离AE=1.8m;当他从A处摆动到A′处时,有A'B⊥AB.
(1)求A′到BD的距离;
(2)求A′到地面的距离.

查看答案和解析>>
科目: 来源: 题型:
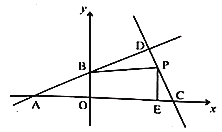
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴,
轴,![]() 轴的交点分别为
轴的交点分别为![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,两条直线的交点为
,两条直线的交点为![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.
![]() 求
求![]() 的面积;
的面积;
![]() 在线段
在线段![]() 上是否存在一点
上是否存在一点![]() ,使四边形
,使四边形![]() 为矩形,若存在,求出
为矩形,若存在,求出![]() 点坐标:若不存在,请说明理由;
点坐标:若不存在,请说明理由;
![]() 若四边形
若四边形![]() 的面积为
的面积为![]() ,设
,设![]() 点的坐标为
点的坐标为![]() ,求出
,求出![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
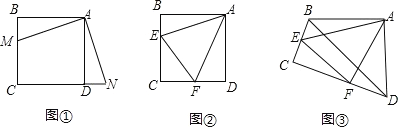
【题目】(1)如图①,点 M 是正方形 ABCD 的边 BC 上一点,点 N 是 CD 延长线上一点, 且BM=DN,则线段 AM 与 AN 的关系.
(2)如图②,在正方形 ABCD 中,点 E、F分别在边 BC、CD上,且∠EAF=45°,判断 BE,DF,EF 三条线段的数量关系,并说明理由.
(3)如图③,在四边形 ABCD中,AB=AD,∠BAD=90°,∠ABC+∠ADC=180°,点E、F分别在边 BC、CD 上,且∠EAF=45°,若 BD=5,EF=3,求四边形 BEFD 的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com