
科目: 来源: 题型:
【题目】(1)材料1:一般地,n个相同因数a相乘:![]() 记为
记为 ![]() 如
如![]() ,此时,3叫做以2为底的8的对数,记为log28(即log28=3).那么,log39=________,
,此时,3叫做以2为底的8的对数,记为log28(即log28=3).那么,log39=________,![]() =________;
=________;
(2)材料2:新规定一种运算法则:自然数1到n的连乘积用n!表示,例如:1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24,…在这种规定下,请你解决下列问题:
①算5!=________;
②已知x为整数,求出满足该等式的![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠A=55°,将△ABC沿DE翻折后,点A落在BC边上的点A′处.如果∠A′EC=70°,那么∠A′DB的度数为( )
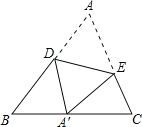
A. 35°B. 40°C. 45°D. 50°
查看答案和解析>>
科目: 来源: 题型:
【题目】下列各选项中所列举的两个变量之间的关系,是反比例函数关系的是( )
A. 直角三角形中,30°角所对的直角边长y与斜边长x之间的关系
B. 等腰三角形中顶角与底角之间的关系
C. 圆的面积S与它的直径d之间的关系
D. 面积为20 cm2的菱形,其中一条对角线长y与另一条对角线长x之间的关系
查看答案和解析>>
科目: 来源: 题型:
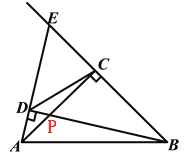
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=![]() ,点P是AC边上的一动点(点P不与端点A、C重合),过点A作AE⊥BP于D,交BC的延长线于点E.
,点P是AC边上的一动点(点P不与端点A、C重合),过点A作AE⊥BP于D,交BC的延长线于点E.
(1)求证:△ACE≌△BCP;
(2)在点P的移动过程中,若AD=DC,试求CP的长;
(3)试探索:在点P的移动过程中,∠ADC的大小是否保持不变?若保持不变,请求出∠ADC的大小;若有变化,请说明变化情况.
查看答案和解析>>
科目: 来源: 题型:
【题目】解密数学魔术:魔术师请观众心想一个数,然后将这个数按以下步骤操作:![]()
魔术师能立刻说出观众想的那个数.
(1)如果小玲想的数是-1,那么她告诉魔术师的结果应该是 ;
(2)如果小明想了一个数计算后,告诉魔术师结果为93,那么魔术师立刻说出小明想的那个数是 ;
(3)观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数.若设观众心想的数为a,请通过计算解密这个魔术的奥妙.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料
利用完全平方公式,将多项式x2+bx+c变形为(x+m)2+n的形式,然后由(x+m)2≥0就可求出多项式x2+bx+c的最小值.
例题:求x2-12x+37的最小值.
解:x2-12x+37=x2-2x·6+62-62+37=(x-6)2+1,
因为不论x取何值,(x-6)2总是非负数,即(x-6)2≥0,
所以(x-6)2+1≥1.
所以当x=6时,x2-12x+37有最小值,最小值是1.
根据上述材料,解答下列问题:
(1)填空:x2-8x+_________=(x-_______)2,
(2)将x2+10x-2变形为(x+m)2+n的形式,并求出x2+10x-2的最小值,
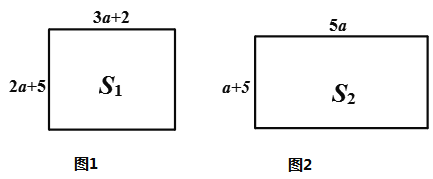
(3)如图①所示的长方形边长分别是2a+5、3a+2,面积为S1:如图②所示的长方形边长分别是5a、a+5,面积为S2. 试比较S1与S2的大小,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
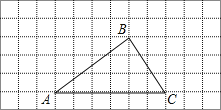
【题目】在如图所示的方格纸中,每个小正方形的边长为1,每个小正方形的顶点都叫做格点.△ABC的顶点A、B、C都在格点上.
(1)过B作AC的平行线BD.
(2)作出表示B到AC的距离的线段BE.
(3)线段BE与BC的大小关系是:BE BC(填“>”、“<”、“=”).
(4)△ABC的面积为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】点![]() 从数轴上表示+2的点开始移动,第1次向左移动1个单位,第2次向右移动2个单位;第3次向左移动3个单位,第4次向右移动4个单位;第5次向左移动5个单位……
从数轴上表示+2的点开始移动,第1次向左移动1个单位,第2次向右移动2个单位;第3次向左移动3个单位,第4次向右移动4个单位;第5次向左移动5个单位……
(1)写出第7次移动后这个点在数轴上表示的数为 ;
(2)直接写出第![]() 次移动后这个点在数轴上表示的数为 ;
次移动后这个点在数轴上表示的数为 ;
(3)如果第![]() 次移动后这个点在数轴上表示的数为56,求
次移动后这个点在数轴上表示的数为56,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,A(-4,![]() ),B(-1,2)是一次函数y=kx+b的图像与反比例函数
),B(-1,2)是一次函数y=kx+b的图像与反比例函数![]() (m≠0,m<0)的函数图像的两个交点,AC⊥x轴于点C,BD⊥y轴于点D
(m≠0,m<0)的函数图像的两个交点,AC⊥x轴于点C,BD⊥y轴于点D
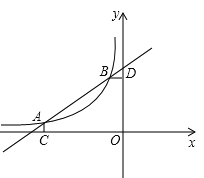
(1)根据函数图像直接回答问题:在第二象限内,当x取何值时,一次函数的值大于反比例函数的值?
(2)求一次函数的表达式及m的值;
(3)点P是线段AB上一点,连接PC,PD,若△PCA和△PBD的面积相等,求点P的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com