
科目: 来源: 题型:
【题目】2017年5月25日,中国国际大数据产业博览会在贵阳会展中心开幕,博览会设了编号为1~6号展厅共6个,小雨一家计划利用两天时间参观其中两个展厅:第一天从6个展厅中随机选择一个,第二天从余下的5个展厅中再随机选择一个,且每个展厅被选中的机会均等.
(1)第一天,1号展厅没有被选中的概率是 ;
(2)利用列表或画树状图的方法求两天中4号展厅被选中的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】(阅读材料)解方程(x-1)2-5(x-1)+4=0时,我们发现:先将x-1看作一个整体,然后设x-1=y.……①,那么原方程可化为y2-5y+4=0,解得y1=1,y2=4.当y=1时,x-1=1,则x=2;当y=4时,x-1=4,则x=5,故原方程的解为x1=2,x2=5.
上述解题过程,在由原方程得到方程①的过程中,运用了“换元法”达到了解方程的目的,体现了转化的数学思想.
(解决问题)
(1)请利用以上知识解方程:(3x+5)2-4(3x+5)+3=0;
(2)在△ABC中,∠C=90°,两条直角边的长分别为a,b,斜边的长为c,且(a2+b2)(a2+b2+1)=12,求斜边c的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】以下说法合理的是( )
A. 小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是![]()
B. 某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖
C. 某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是![]()
D. 小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的方程(x-3)(x-2)-p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1、x2,且满足x12+x22=3 x1x2,求实数p的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】把长为22 cm的金属丝围成一个一条边长为x(cm),面积为S(cm2)的矩形框.
(1)写出用x表示S的式子;
(2)在(1)中,若S=10 cm2,请求出矩形的长和宽.
查看答案和解析>>
科目: 来源: 题型:
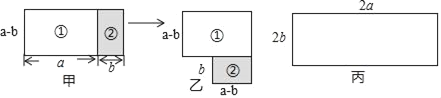
【题目】如图所示,图甲由长方形①,长方形②组成,图甲通过移动长方形②得到图乙.
(1)S甲= ,S乙= (用含a、b的代数式分别表示);
(2)利用(1)的结果,说明a2、b2、(a+b)(a﹣b)的等量关系;
(3)现有一块如图丙尺寸的长方形纸片,请通过对它分割,再对分割的各部分移动,组成新的图形,画出图形,利用图形说明(a+b)2、(a﹣b)2、ab三者的等量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】如果一个正整数可以表示为两个连续奇数的平方差,那么称该正整数为“和谐数”如(8=32﹣12,16=52﹣32,即8,16均为“和谐数”),在不超过2017的正整数中,所有的“和谐数”之和为( )
A. 255054 B. 255064 C. 250554 D. 255024
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF=_____________.

查看答案和解析>>
科目: 来源: 题型:
【题目】在数学问题中,我们常用几何方法解决代数问题,借助数形结合的方法使复杂问题简单化.
材料一:我们知道|a|的几何意义是:数轴上表示数a的点到原点的距离;|a﹣b|的几何意义是:数轴上表示数a,b的两点之间的距离;|a+b|的几何意义是:数轴上表示数a,﹣b的两点之间的距离;根据绝对值的几何意义,我们可以求出以下方程的解.
(1)|x﹣3|=4
解:由绝对值的几何意义知:
在数轴上x表示的点到3的距离等于4
∴x1=3+4=7,x2=3﹣4=﹣1
(2)|x+2|=5
解:∵|x+2|=|x﹣(﹣2)|,∴其绝对值的几何意义为:在数轴上x表示的点到﹣2的距离等于5.∴x1=﹣2+5=3,x2=﹣2﹣5=﹣7
材料二:如何求|x﹣1|+|x+2|的最小值.
由|x﹣1|+|x+2|的几何意义是数轴上表示数x的点到表示数1和﹣2两点的距离的和,要使和最小,则表示数x的这点必在﹣2和1之间(包括这两个端点)取值.
∴|x﹣1|+|x+2|的最小值是3;由此可求解方程|x﹣1|+|x+2|=4,把数轴上表示x的点记为点P,由绝对值的几何意义知:当﹣2≤x≤1时,|x﹣1|+|x+2|恒有最小值3,所以要使|x﹣1|+|x+2|=4成立,则点P必在﹣2的左边或1的右边,且到表示数﹣2或1的点的距离均为0.5个单位.
故方程|x﹣1|+|x+2|=4的解为:x1=﹣2﹣0.5=﹣2.5,x2=1+0.5=1.5.
阅读以上材料,解决以下问题:
(1)填空:|x﹣3|+|x+2|的最小值为 ;
(2)已知有理数x满足:|x+3|+|x﹣10|=15,有理数y使得|y﹣3|+|y+2|+|y﹣5|的值最小,求x﹣y的值.
(3)试找到符合条件的x,使|x﹣1|+|x﹣2|+…+|x﹣n|的值最小,并求出此时的最小值及x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com