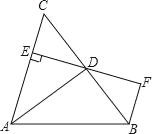
A. ①②③④ B. ①②④ C. ①②③ D. ②③④

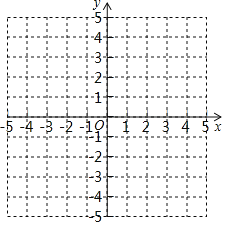
（1）依据表中给出的对应关系写出函数解析式，并在给出的坐标系中画出大致图象；

（2）在这个函数图象上有一点P（x，y）（x＜0），过点P分别作x轴和y轴的垂线，并延长与直线y=x﹣2交于A、B两点，若△PAB的面积等于，求出P点坐标．

【题目】如图，把一个边长为的大正方形，剪去一个边长为的小正方形后，得到图①，称之为“前世”，然后再剪拼成一个新长方形即图②，称之为“今生”，请你解答下面的问题：

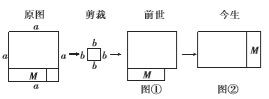
（1）“前世”图①的面积与“今生”图②新长方形的面积______；

（2）根据图形面积的和差关系直接写出“前世”图①的面积为_______，标明“今生”图②新长方形的长为______、宽为_______、面积为_______；

（3）“形缺数时少直观，数缺形时少形象”它体现了数学的数形结合思想，由（1）和（2）图形面积的计算，形象地验证了代数中的一个乘法公式：______；

（4）利用本题所得公式计算：．

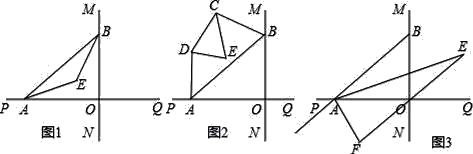
（1）如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．

（2）如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，又DE、CE分别是∠ADC和∠BCD的角平分线，点A、B在运动的过程中，∠CED的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值．

（3）如图3，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F，在△AEF中，如果有一个角是另一个角的3倍，试求∠ABO的度数．

（1）利用尺规作图作边BC的高AD，垂足为D（保留作图痕迹，不写作法）；

（2）求证：BD=CD．

（3）如果三角形的周长是22，一边长为5，求它的另外两边长．

如果两个两位数的十位数字相同，个位数字相加为10，那么能立即说出这两个两位数的乘积，如果这两个两位数分别写作和（即十位数字为，个位数字分别为、，，），那么它们的乘积是一个4位数，前两位数字是和的乘积，后两位数字就是和的乘积，如：，．

（1）________；

（2）设这两个两位数的十位数字为，个位数字分别为和，，通过计算验证这两个两位数的乘积为．

【题目】观察下列各式：···①，···②，…③，…

探索以上式子的规律．

（1）第7个式子是_______；

（2）试写出第个等式，并说明第个等式成立；

（3）根据以上规律写出第2019个式子：______．

【题目】如图，已知数轴上依次有三点 A、B、C，点 B 对应的数是，且点 B 到点A、C的距离均为600.

(1)写出点A所对应的数；

(2)若动点P、Q分别从B、C两点同时向右运动，点 P、Q 的速度分别为 10 单位长度每秒、5单位长度每秒，问多少秒时点P与点Q重合；

(3)若动点P、Q分别从A、C两点相向而行，点P运动20秒后，点Q开始运动，点P、Q的速度分别为10单位长度每秒、5单位长度每秒，问点 P 运动多少秒时P，Q两点的距离为200.