
科目: 来源: 题型:
【题目】如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为( ).

A.126°B.110°C.108°D.90°
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的方程(k﹣2)2x2+(2k+1)x+1=0有实数解,且反比例函数y=![]() 的图象经过第二、四象限,若k是常数,则k的值为( )
的图象经过第二、四象限,若k是常数,则k的值为( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目: 来源: 题型:
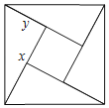
【题目】如图,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边
表示直角三角形的两直角边![]() ,下列四个说法:①
,下列四个说法:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中说法正确的是
;其中说法正确的是![]()
![]()
A. ①②B. ①②③C. ①②④D. ①②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式了的平方,如3+2![]() =(1+
=(1+![]() )2.善于思考的小明进行了以下探索:
)2.善于思考的小明进行了以下探索:
若设a+b![]() =(m+n
=(m+n![]() )2=m2+2n2+2mn
)2=m2+2n2+2mn![]() (其中a、b、m、n均为整数),
(其中a、b、m、n均为整数),
则有a=m2+2n2,b=2mn.
这样小明就找到了一种把类似a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)若a+b![]() =(m+n
=(m+n![]() )2,当a、b、m、n均为整数时,用含m、n的式子分别表示a、b,得:a= ,b= ;
)2,当a、b、m、n均为整数时,用含m、n的式子分别表示a、b,得:a= ,b= ;
(2)若a+6![]() =(m+n
=(m+n![]() )2,且a、m、n均为正整数,求a的值;
)2,且a、m、n均为正整数,求a的值;
(3)化简:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() 与x轴交于点A,B(点A在点B的左边),与y轴交于点C,点D是该抛物线的顶点.
与x轴交于点A,B(点A在点B的左边),与y轴交于点C,点D是该抛物线的顶点.
(1)如图1,连接CD,求线段CD的长;
(2)如图2,点P是直线AC上方抛物线上一点,PF⊥x轴于点F,PF与线段AC交于点E;将线段OB沿x轴左右平移,线段OB的对应线段是O1B1,当PE+![]() EC的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标;
EC的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标;
(3)如图3,点H是线段AB的中点,连接CH,将△OBC沿直线CH翻折至△O2B2C的位置,再将△O2B2C绕点B2旋转一周在旋转过程中,点O2,C的对应点分别是点O3,C1,直线O3C1分别与直线AC,x轴交于点M,N.那么,在△O2B2C的整个旋转过程中,是否存在恰当的位置,使△AMN是以MN为腰的等腰三角形?若存在,请直接写出所有符合条件的线段O2M的长;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
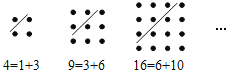
A.13=3+10B.25=9+16C.36=15+21D.49=18+31
查看答案和解析>>
科目: 来源: 题型:
【题目】已知一列数:1,―2,3,―4,5,―6,7,… 将这列数排成下列形式:
第1行 1
第2行 -2 3
第3行 -4 5 -6
第4行 7 -8 9 -10
第5行 11 -12 13 -14 15
… …
按照上述规律排下去,那么第10行从左边数第5个数等于
A.50B.-50C.60D.-60
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在ABCD中,∠ACB=45°,点E在对角线AC上,BE=BA,BF⊥AC于点F,BF的延长线交AD于点G.点H在BC的延长线上,且CH=AG,连接EH.
(1)若BC=12![]() ,AB=13,求AF的长;
,AB=13,求AF的长;
(2)求证:EB=EH.

查看答案和解析>>
科目: 来源: 题型:
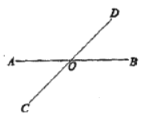
【题目】如图,直线![]() 、
、![]() 与相交于点
与相交于点![]() ,形成了
,形成了![]() 个角.
个角.
(1)图中,![]() 与
与![]() 有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.这样的邻补角还有以下几对,它们分别是____________、__________、______________.
有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.这样的邻补角还有以下几对,它们分别是____________、__________、______________.
(2)图中,![]() 与
与![]() 有一个公共顶点,且
有一个公共顶点,且![]() 的两边分别是
的两边分别是![]() 的反向延长线,具有这种位置关系的两个角,互为对顶角.这样的对顶角还有一对,它们是________与___________.
的反向延长线,具有这种位置关系的两个角,互为对顶角.这样的对顶角还有一对,它们是________与___________.
(3)因为![]() ______________,
______________,![]() ____________所以
____________所以![]() ______
______![]() (填写
(填写![]() 或
或![]() 或
或![]() )理由是____________由此能得到的结论是:对顶角_____________
)理由是____________由此能得到的结论是:对顶角_____________
(4)用您所学知识可得![]() ___________(精确到度).
___________(精确到度).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com