
科目: 来源: 题型:
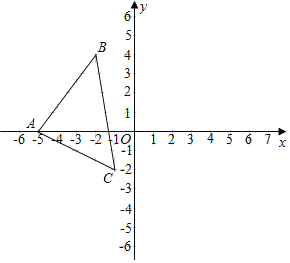
【题目】△ABC三顶点A(﹣5,0)、B(﹣2,4)、C(﹣1,﹣2),△A'B'C'与△ABC关于y轴对称.
(1)直接写出A'、B'、C'的坐标;
(2)画出△A'B'C';
(3)求△ABC的面积.
查看答案和解析>>
科目: 来源: 题型:
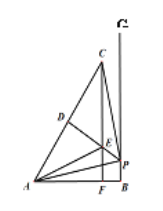
【题目】如图,线段AB=8,射线BG⊥AB,P为射线BG上一点,连接AP,作AP⊥CP且AP=CP,连接AC,PD平分∠APC,且C、D与点B在AP两侧,在线段DP取一点E,使∠EAP=∠BAP,连接CE与线段AB相交于点F(点F与点A、B不重合).
(1)求证:△AEP≌△CEP;
(2)判断CF与AB的位置关系,并说明理由;
(3)求△AEF的周长.
查看答案和解析>>
科目: 来源: 题型:
【题目】(问题引领)
问题1:如图1,在四边形ABCD中,CB=CD,∠B=∠ADC=90°,∠BCD=120°.E,F分别是AB,AD上的点.且∠ECF=60°.探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结CG,先证明△CBE≌△CDG,再证明△CEF≌△CGF.他得出的正确结论是 .
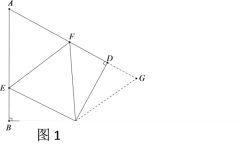
(探究思考)
问题2:如图2,若将问题1的条件改为:四边形ABCD中,CB=CD,∠ABC+∠ADC=180°,∠ECF=![]() ∠BCD,问题1的结论是否仍然成立?请说明理由.
∠BCD,问题1的结论是否仍然成立?请说明理由.
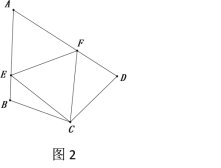
(拓展延伸)
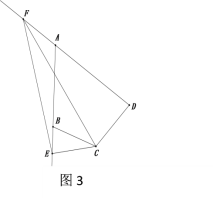
问题3:如图3,在问题2的条件下,若点E在AB的延长线上,点F在DA的延长线上,若BE=2,DF=8,求EF的长(请直接写出答案)
查看答案和解析>>
科目: 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() .给出定义如下:使等式
.给出定义如下:使等式![]() 成立的一对有理数
成立的一对有理数![]() ,
,![]() 为“共生有理数对”,记为
为“共生有理数对”,记为![]() .如:数对
.如:数对![]() ,
,![]() 都有“共生有理数对”.
都有“共生有理数对”.
(1)数对![]() ,
,![]() 中是“共生有理数对”的是 .
中是“共生有理数对”的是 .
(2)请再写出另外一对符合条件的“共生有理数对” (不能与题目中已有的重复).
(3)小丁说:“若![]() 是‘共生有理数对’,则
是‘共生有理数对’,则![]() 一定是‘共生有理数对’.”请你用(2)中写出的“共生有理数对”验证小丁的说法.
一定是‘共生有理数对’.”请你用(2)中写出的“共生有理数对”验证小丁的说法.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的一元二次方程(x﹣3)(x﹣2)=|m|.
(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
查看答案和解析>>
科目: 来源: 题型:
【题目】荣获“中华名果”称号的![]() 市脐橙果大形正,橙红鲜艳,含果汁55%以上,深受广大“吃货”的喜爱.现有20筐
市脐橙果大形正,橙红鲜艳,含果汁55%以上,深受广大“吃货”的喜爱.现有20筐![]() 市脐橙,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
市脐橙,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值 (单位:千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)在这20筐![]() 市脐橙中,最重的一筐比最轻的一筐重多少千克?
市脐橙中,最重的一筐比最轻的一筐重多少千克?
(2)与标准重量比较,20筐![]() 市脐橙总计超过或不足多少千克?
市脐橙总计超过或不足多少千克?
(3)若![]() 市脐橙每千克售价8元,则这20筐
市脐橙每千克售价8元,则这20筐![]() 市脐橙可卖多少元?
市脐橙可卖多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=![]() c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+![]() cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.

请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+![]() cx+b=0必有实数根;
cx+b=0必有实数根;
若x=1是“勾系一元二次方程”ax+![]() cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是![]() ,求△ABC面积.
,求△ABC面积.
查看答案和解析>>
科目: 来源: 题型:
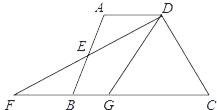
【题目】如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
查看答案和解析>>
科目: 来源: 题型:
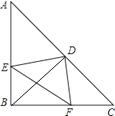
【题目】如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边中点,过D点作DE⊥DF,交AB于E,交BC于F,连接BD.
(1)求证:△CDF≌△BED
(2)若AE=4,FC=3,求AB长
查看答案和解析>>
科目: 来源: 题型:
【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;
![]()
(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com