(1)根据图(2)，写出一个多项式乘以多项式的等式.

(2)从A、B两题中任选一题作答.

A．请画一个几何图形，表示(x+p)(x+q)=x2+(p+q)x+pq，并仿照上图标明相应的字母.

B. 请画一个几何图形，表示(x-p)(x-q)=x2-(p+q)x+pq，并仿照上图标明相应的字母.

(1)利用尺规完成以下作图，并保留作图痕迹．(不要求写作法)

①作BE平分∠ABD交AC于点E；

②在BA的延长线上截取AF=BA，连接EF；

(2)判断△BEF的形状，并说明理由．

(1)作出△ABC关于x轴对称的图形；

(2)写出A、B、C的对应点A′、B′、C′的坐标；

(3)在x轴上画出点Q，使△QAC的周长最小

A. 2 B. 6 C. 3 D.

A. △ABD与△ABC的周长相等

B. △ABD与△ABC的面积相等

C. 菱形的周长等于两条对角线之和的两倍

D. 菱形的面积等于两条对角线之积的两倍

　A．1 B． C． 2 D．＋1

求x+6x+11的最小值．

解：x+6x+11

=x2+6x+9+2

=（x+3）2+2

由于（x+3）2的值必定为非负数，所以（x+3）2+2，即x2+6x+11的最小值为2．

（二）解决问题

（1）若m2+2mn+2n2-6n+9=0，求（）-3的值；

（2）对于多项式x2+y-2x+2y+5，当x，y取何值时有最小值，最小值为多少？

（1）求∠AOE的度数；

（2）若OF平分∠BOE，问：OB是∠DOF的平分线吗？试说明理由．

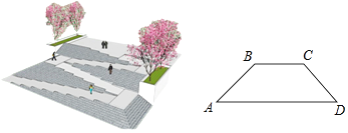
（1）选择哪个坡度建设轮椅专用坡道AB是符合要求的？说明理由；

（2）求斜坡底部点A与台阶底部点D的水平距离AD．

（1）如果上述仰角与俯角分别为30°与60°，且该楼的高度为30米，求该时刻无人机的竖直高度CD；

（2）如图2，如果上述仰角与俯角分别为α与β，且该楼的高度为m米．求用α、β、m表示该时刻无人机的竖直高度CD．