
科目: 来源: 题型:
【题目】如图,∠AOB=20°,M,N分別是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=α,∠OQN=β,当MP+PQ+QN最小时,则关于α,β的数量关系正确的是( )

A.β﹣α=30°B.β﹣α=40°C.β+α=180°D.β+α=200°
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF交AB于E,交BC于F,若四边形BFDE的面积为16,则AB的长为( )

A.8B.10C.12D.16
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,AD是∠BAC的角平分线,DE⊥AB,垂足为点E,DE=1,BE=![]() ,则△ABC的周长是( )
,则△ABC的周长是( )

A.6+![]() B.3+2
B.3+2![]() C.6+2
C.6+2![]() D.3+3
D.3+3![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ACB>∠ABC,三条内角平分线AD,BE,CF相交于点I.

(1)若∠ABE=25°,求∠DIC的度数;
(2)在(1)的条件下,图中互余的角有多少对?列举出来;
(3)过I点作IH⊥BC,垂足为H,试问∠BID与∠HIC相等吗?为什么?
(4)G是AD延长线上一点,过G点作GP⊥BC,垂足为P,试探究∠G与∠ABC,∠ACB之间的数量关系,直接写出结论,不需证明.
查看答案和解析>>
科目: 来源: 题型:
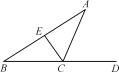
【题目】如图,CA平分∠DCE,且与BE的延长线相交于点A.
(1)若∠A=35°,∠B=30°,则∠BEC= ;(直接在横线上填写度数)
(2)小明经过改变∠A,∠B的度数进行多次探究,得出∠A,∠B,∠BEC三个角之间存在固定的数量关系,请你用一个等式表示出这个关系,并进行证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,矩形ABCD中,E是AD的中点,以点E直角顶点的直角三角形EFG的两边EF,EG分别过点B,C,∠F=30°.
(1)求证:BE=CE
(2)将△EFG绕点E按顺时针方向旋转,当旋转到EF与AD重合时停止转动.若EF,EG分别与AB,BC相交于点M,N.(如图2)
①求证:△BEM≌△CEN;
②若AB=2,求△BMN面积的最大值;
③当旋转停止时,点B恰好在FG上(如图3),求sin∠EBG的值.



查看答案和解析>>
科目: 来源: 题型:
【题目】益马高速通车后,将桃江马迹塘的农产品运往益阳的运输成本大大降低。马迹塘一农户需要将A,B两种农产品定期运往益阳某加工厂,每次运输A,B产品的件数不变,原来每运一次的运费是1200元,现在每运一次的运费比原来减少了300元,A,B两种产品原来的运费和现在的运费(单位:元∕件)如下表所示:
品种 | A | B |
原来的运费 | 45 | 25 |
现在的运费 | 30 | 20 |
(1)求每次运输的农产品中A,B产品各有多少件?
(2)由于该农户诚实守信,产品质量好,加工厂决定提高该农户的供货量,每次运送的总件数增加8件,但总件数中B产品的件数不得超过A产品件数的2倍,问产品件数增加后,每次运费最少需要多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中有三点(1,2),(3,1),(-2,-1),其中有两点同时在反比例函数![]() 的图象上,将这两点分别记为A,B,另一点记为C,
的图象上,将这两点分别记为A,B,另一点记为C,
(1)求出![]() 的值;
的值;
(2)求直线AB对应的一次函数的表达式;
(3)设点C关于直线AB的对称点为D,P是![]() 轴上的一个动点,直接写出PC+PD的最小值(不必说明理由).
轴上的一个动点,直接写出PC+PD的最小值(不必说明理由).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com