
科目: 来源: 题型:
【题目】为响应环保组织提出的“低碳生活”的号召,李明决定不开汽车而改骑自行车上班.有一天,李明骑自行车从家里到工厂上班,途中因自行车发生故障,修车耽误了一段时间,车修好后继续骑行,直至到达工厂(假设在骑自行车过程中匀速行驶).李明离家的距离y(米)与离家时间x(分钟)的关系表示如下图:
(1)李明从家出发到出现故障时的速度为 米/分钟;
(2)李明修车用时 分钟;
(3)求线段OA所对应的函数关系式(不要求写出自变量的取值范围).

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线y=-x2+mx+3与x轴交于点A、B两点,与y轴交于C点,点B的坐标为(3,0),抛物线与直线y=-![]() x+3交于C、D两点.连接BD、AD.
x+3交于C、D两点.连接BD、AD.

(1)求m的值.
(2)抛物线上有一点P,满足S△ABP=4S△ABD,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-3,0),B(-3,-4),C(-1,-4).
(1)求△ABC的面积;
(2)在图中作出△ABC关于x轴对称的图形△DEF,点A、B、C的对称点分别为D、E、F,并写出D、E、F的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】一位运动员在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离是2.5m时,达到最大高度3.5m,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式.
(2)该运动员身高1.8m,在这次跳投中,球在头顶上0.25m处出手,
问:球出手时,他距离地面的高度是多少?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:
①b2=4ac;②abc>0;③a>c;④4a﹣2b+c>0,其中正确的个数有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】作出函数y=2-2x的图象,并根据图象回答下列问题:
(1)y的值随x的增大而____,减小而____;
(2)图象与x轴的交点坐标是___;与y轴的交点坐标是____;
(3)函数y=2-2x的图象与坐标轴所围成的三角形的面积是多少?

查看答案和解析>>
科目: 来源: 题型:
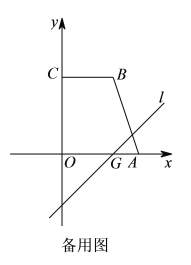
【题目】如图,抛物线y=ax2+bx+6过点A(6,0),B(4,6),与y轴交于点C.
(1)求该抛物线的解析式;
(2)如图1,直线l的解析式为y=x,抛物线的对称轴与线段BC交于点P,过点P作直线l的垂线,垂足为点H,连接OP,求△OPH的面积;
(3)把图1中的直线y=x向下平移4个单位长度得到直线y=x-4,如图2,直线y=x-4与x轴交于点G.点P是四边形ABCO边上的一点,过点P分别作x轴、直线l的垂线,垂足分别为点E,F.是否存在点P,使得以P,E,F为顶点的三角形是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.


查看答案和解析>>
科目: 来源: 题型:
【题目】如图,把![]() 向上平移4个单位长度,再向右平移3个单位长度得
向上平移4个单位长度,再向右平移3个单位长度得![]() ,其中
,其中![]() ,
,![]() ,
,![]() .
.
(1)在图上画出![]() ;
;
(2)写出点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(3)请直接写出线段![]() 在两次平移中扫过的总面积.
在两次平移中扫过的总面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】在一次消防演习中,消防员架起一架25米长的云梯,如图斜靠在一面墙上,梯子底端离墙7米.
(1)求这个梯子的顶端距地面有多高?
(2)如果消防员接到命令,要求梯子的顶端下降4米(云梯长度不变),那么云梯的底部在水平方向应滑动多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com