
科目: 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(3,0),B(﹣1,0),C(0,﹣3).
(1)求该抛物线的解析式;
(2)若以点A为圆心的圆与直线BC相切于点M,求切点M的坐标;
(3)若点Q在x轴上,点P在抛物线上,是否存在以点B,C,Q,P为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】知识背景
当a>0且x>0时,因为(![]() ﹣
﹣![]() )2≥0,所以x﹣2
)2≥0,所以x﹣2![]() +
+![]() ≥0,从而x+
≥0,从而x+![]() (当x=
(当x=![]() 时取等号).
时取等号).
设函数y=x+![]() (a>0,x>0),由上述结论可知:当x=
(a>0,x>0),由上述结论可知:当x=![]() 时,该函数有最小值为2
时,该函数有最小值为2![]() .
.
应用举例
已知函数为y1=x(x>0)与函数y2=![]() (x>0),则当x=
(x>0),则当x=![]() =2时,y1+y2=x+
=2时,y1+y2=x+![]() 有最小值为2
有最小值为2![]() =4.
=4.
解决问题
(1)已知函数为y1=x+3(x>﹣3)与函数y2=(x+3)2+9(x>﹣3),当x取何值时,![]() 有最小值?最小值是多少?
有最小值?最小值是多少?
(2)已知某设备租赁使用成本包含以下三部分:一是设备的安装调试费用,共490元;二是设备的租赁使用费用,每天200元;三是设备的折旧费用,它与使用天数的平方成正比,比例系数为0.001.若设该设备的租赁使用天数为x天,则当x取何值时,该设备平均每天的租货使用成本最低?最低是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别是边AD,BC的中点,连接DF,过点E作EH⊥DF,垂足为H,EH的延长线交DC于点G.
(1)猜想DG与CF的数量关系,并证明你的结论;
(2)过点H作MN∥CD,分别交AD,BC于点M,N,若正方形ABCD的边长为10,点P是MN上一点,求△PDC周长的最小值.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知在等腰直角△ABC中,∠BAC=90°,点D从点B出发沿射线BC方向移动.在AD右侧以AD为腰作等腰直角△ADE,∠DAE=90°.连接CE.

(1)求证:△ACE≌△ABD;
(2)点D在移动过程中,请猜想CE,CD,DE之间的数量关系,并说明理由;
(3)若AC=![]() ,当CD=1时,结合图形,请直接写出DE的长 .
,当CD=1时,结合图形,请直接写出DE的长 .
查看答案和解析>>
科目: 来源: 题型:
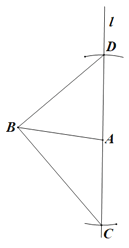
【题目】在一次研究性学习活动中,同学们看到了工人师傅在木板上画一个直角三角形的过程(如图所示):画线段AB,过点A任作一条直线l,以点A为圆心,以AB长为半径画弧,与直线l相交于两点C、D,连接BC和BD.则△BCD就是直角三角形.
(1)请你说明△BCD是直角三角形的道理;
(2)请利用上述方法作一个直角三角形,使其中一个锐角为60°(不写作法,保留作图
痕迹,在图中注明60°的角).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.

(1)说明BE=CF的理由;
(2)如果AB=5,AC=3,求AE、BE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com