
科目: 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5。一只蚂蚁如果要沿着长方体的表面从点A爬到点B,爬行的最短路程是( )
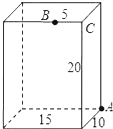
A.25B.![]() C.35D.无法确定
C.35D.无法确定
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,把n个边长为1的正方形拼接成一排,求得tan∠BA1C=1,tan∠BA2C=![]() ,tan∠BA3C=
,tan∠BA3C=![]() ,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).
,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,D是BC中点,AD⊥BC,E是BC上除B,D,C外任意一点,根据“SAS”,可证明![]() ,所以AB=AC,∠B=∠C.在△ABE和△ACE中,
,所以AB=AC,∠B=∠C.在△ABE和△ACE中,![]() ,不能证明
,不能证明![]() ,因为这是“SSA”的情形,
,因为这是“SSA”的情形,![]() 是钝角三角形,
是钝角三角形,![]() 是锐角三角形,它们不可能全等.如果两个三角形都是直角三角形,“SSA”就变成“HL”,就可以用来证明两个三角形全等.同样,如果我们知道两个三角形都是钝角三角形或锐角三角形,并且它们满足“SSA”的情形,也是一定能全等的,但必须通过构造直角三角形来间接证明.
是锐角三角形,它们不可能全等.如果两个三角形都是直角三角形,“SSA”就变成“HL”,就可以用来证明两个三角形全等.同样,如果我们知道两个三角形都是钝角三角形或锐角三角形,并且它们满足“SSA”的情形,也是一定能全等的,但必须通过构造直角三角形来间接证明.
问题:已知,如图2,AD=AC,![]() ,
,
(1)根据现有条件直接证明![]() ,可以吗?为什么?
,可以吗?为什么?
(2)求证:![]() .
.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,tanA=![]() .点D,E分别是边BC,AC上的点,且∠EDC=∠A.将△ABC沿DE所在直线对折,若点C恰好落在边AB上,则DE的长为___.
.点D,E分别是边BC,AC上的点,且∠EDC=∠A.将△ABC沿DE所在直线对折,若点C恰好落在边AB上,则DE的长为___.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,C是线段AB上一点,分别以AC.BC为边作等边△DAC和等边△ECB,AE与BD.CD相交于点F、G,CE与BD相交于点H.
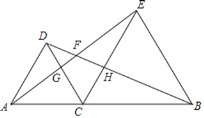
(1)求证:△ACE≌△DCB;
(2)求∠AFB的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某人在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i为1∶![]() ,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.则A,B两点间的距离是( )
,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.则A,B两点间的距离是( )
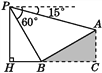
A. 15米 B. 20![]() 米 C. 20
米 C. 20![]() 米 D. 10
米 D. 10![]() 米
米
查看答案和解析>>
科目: 来源: 题型:
【题目】为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:①BC,∠ACB; ②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B间距离的有【 】
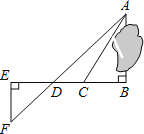
A.1组 B.2组 C.3组 D.4组
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是
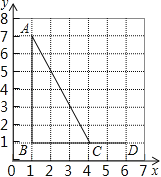
A.(6,0) B.(6,3) C.(6,5) D.(4,2)
查看答案和解析>>
科目: 来源: 题型:
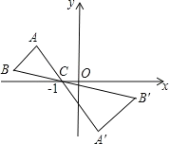
【题目】如图,△ABC中,A、B两个顶点在![]() 轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论正确的是( )

A. ∠E=2∠K B. BC=2HI C. 六边形ABCDEF的周长=六边形GHIJKL的周长 D. S六边形ABCDEF=2S六边形GHIJKL
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com