
科目: 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AC﹣AB=2BE中正确的是_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】自![]() 年
年![]() 月
月![]() 日零时起,高铁开通,某旅行社为吸引广大市民组团去仙都旅游,推出了如下收费标准:如果人数不超过
日零时起,高铁开通,某旅行社为吸引广大市民组团去仙都旅游,推出了如下收费标准:如果人数不超过![]() 人,人均旅游费用为
人,人均旅游费用为![]() 元,如果人数超过
元,如果人数超过![]() 人,每增加
人,每增加![]() 人,人均旅游费用降低
人,人均旅游费用降低![]() 元,但人均旅游费用不得低于
元,但人均旅游费用不得低于![]() 元.
元.
![]() 如果某单位组织
如果某单位组织![]() 人参加仙都旅游,那么需支付旅行社旅游费用________元;
人参加仙都旅游,那么需支付旅行社旅游费用________元;
![]() 现某单位组织员工去仙都旅游,共支付给该旅行社旅游费用
现某单位组织员工去仙都旅游,共支付给该旅行社旅游费用![]() 元,那么该单位有多少名员工参加旅游?
元,那么该单位有多少名员工参加旅游?
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业加工一台大型机械设备润滑用油![]() 千克,用油的重复利用率为
千克,用油的重复利用率为![]() ,按此计算,加工一台大型机械设备的实际耗油量为
,按此计算,加工一台大型机械设备的实际耗油量为![]() 千克.通过技术革新后,不仅降低了润滑用油量,同时也提高了用油的重复利用率,并且发现润滑用油量每减少
千克.通过技术革新后,不仅降低了润滑用油量,同时也提高了用油的重复利用率,并且发现润滑用油量每减少![]() 千克,用油量的重复利用率增加
千克,用油量的重复利用率增加![]() ,这样加工一台大型机械设备的实际耗油量下降到
,这样加工一台大型机械设备的实际耗油量下降到![]() 千克,问技术革新后,加工一台大型机械设备润滑用油量是多少千克?用油的重复利用率是多少?
千克,问技术革新后,加工一台大型机械设备润滑用油量是多少千克?用油的重复利用率是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】若![]() ,
,![]() 是一元二次方程
是一元二次方程![]() 的两根,则有
的两根,则有![]() ,
,![]() ,由上式可知,一元二次方程的两根和、两根积是由方程的系数确定的,我们把这个关系称为一元二次方程根与系数的关系.若
,由上式可知,一元二次方程的两根和、两根积是由方程的系数确定的,我们把这个关系称为一元二次方程根与系数的关系.若![]() ,
,![]() 是方程
是方程![]() 的两根,记
的两根,记![]() ,
,![]() ,…,
,…,![]() ,
,
![]() ________;
________;![]() ________;
________;![]() ________;
________;![]() ________;(直接写出结果)
________;(直接写出结果)
![]() 当
当![]() 为不小于
为不小于![]() 的整数时,由
的整数时,由![]() 猜想
猜想![]() ,
,![]() ,
,![]() 有何关系?
有何关系?
![]() 利用
利用![]() 中猜想求
中猜想求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,D、E、F分别是AC、BC、AB的中点,连接DE.点P从点D出发,沿DE方向匀速运动;同时,点Q从点E出发,沿EB方向匀速运动,两者速度均为1cm/s;当其中一点停止运动时,另外一点也停止运动.连接PQ、PF,设运动时间为ts(0<t<4).解答下列问题:
(1)当t为何值时,△EPQ为等腰三角形?
(2)如图①,设四边形PFBQ的面积为ycm2,求y与t之间的函数关系式;
(3)当t为何值时,四边形PFBQ的面积与△ABC的面积之比为2:5?
(4)如图②,连接FQ,是否存在某一时刻,使得PF与QF互相垂直?若存在,求出此时t的值;若不存,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】(操作发现)
如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.
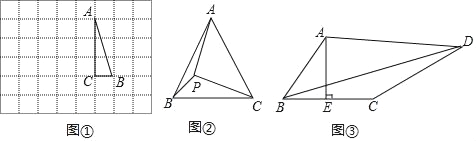
(1)请按要求画图:将△ABC绕点A按逆时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′
(2)在(1)所画图形中,∠AB′B= .
(问题解决)
如图②,在等边三角形ABC中,AC=![]() ,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找线段PA、PC之间的数量关系;
想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找线段PA、PC之间的数量关系;
请参考小明同学的想法,完成该问题的解答过程.(求解一种方法即可)
(灵活运用)
如图③,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=5,AD=kAB(k为常数),直接写出BD的长(用含k的式子表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量m(件)与时间t(天)的关系满足:m=﹣2t+96.且未来40天内,前20天每天的价格y1(元/件)与时间t(天)的函数关系式为y1=![]() t+25(1≤t≤20且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式为y2=﹣
t+25(1≤t≤20且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式为y2=﹣![]() t+40(21≤t<40且t为整数).下面我们就来研究销售这种商品的有关问题
t+40(21≤t<40且t为整数).下面我们就来研究销售这种商品的有关问题
(1)请分别写出未来40天内,前20天和后20天的日销售利润w(元)与时间t的函数关系式;
(2)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中,该公司决定每销售一件商品就捐赠a元利润(a<4)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
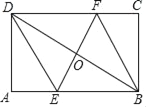
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB、CD边于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)求证:△ADE≌△CBF;
(3)当四边形BEDF是菱形时,直接写出线段EF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,A、B 两点分别位于一个池塘的两端,小明想用绳子测量A、B 间的距离,但绳子不够长,请你利用三角形全等的相关知识帮他设计一种方案测量出A、B间的距离,写出具体的方案,并解释其中的道理,

查看答案和解析>>
科目: 来源: 题型:
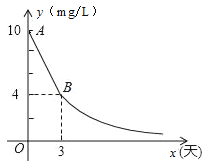
【题目】环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0 mg/L.环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,其中第3天时硫化物的浓度降为4 mg/L.从第3天起所排污水中硫化物的浓度y与时间x满足下面表格中的关系:
时间x(天) | 3 | 4 | 5 | 6 | 8 | …… |
硫化物的浓y(mg/L) | 4 | 3 | 2.4 | 2 | 1.5 |
(1)求整改过程中当0≤x<3时,硫化物的浓度y与时间x的函数表达式;
(2)求整改过程中当x≥3时,硫化物的浓度y与时间x的函数表达式;
(3)该企业所排污水中硫化物的浓度,能否在15天以内不超过最高允许的1.0 mg/L?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com