
科目: 来源: 题型:
【题目】为更好的了解中学生课外阅读的情况,学校团委将初一年级学生一学期阅读课外书籍量分为A(3本以内)、B(3——6本)、C(6——10本)、D(10本以上)四种情况进行了随机调查,并根据调查结果制成了如下两幅不完整的统计图.请结合统计图所给信息解答上列问题:
(1)在扇形统计图中C所占的百分比是多少?
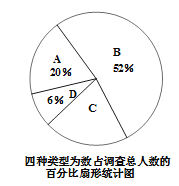
(2)请将折线统计图补充完整;

(3)学校团委欲从课外阅读量在10本以上的同学中随机邀请两位参加学校举办的“书香致远 墨卷至恒”主题读书日的形象大使,请你用列表法或画树状图的方法,求所选出的两位同学恰好都是女生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .
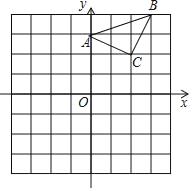
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O =30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2018的纵坐标为______.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知直线l1:y=kx+1,与x轴相交于点A,同时经过点B(2,3),另一条直线l2经过点B,且与x轴相交于点P(m,0).
(1)求l1的解析式;
(2)若S△APB=3,求P的坐标.
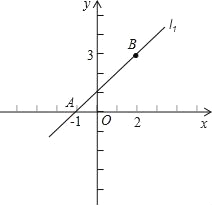
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示的正方形网格中,每个小正方形的边长为1,格点三角形![]() (顶点是网格线的交点的三角形)的顶点
(顶点是网格线的交点的三角形)的顶点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.
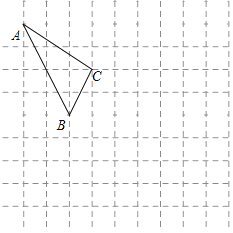
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)点![]() 到
到![]() 轴的距离是 ;
轴的距离是 ;
(3)请作出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(4)写出点![]() 的坐标 .
的坐标 .
查看答案和解析>>
科目: 来源: 题型:
【题目】小丽和小华想利用摸球游戏决定谁去参加市里举办的书法比赛,游戏规则是:在一个不透明的袋子里装有除数字外完全相同的4个小球,上面分别标有数字2,3,4,5.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为偶数,则小丽去参赛;否则小华去参赛.
(1)用列表法或画树状图法,求小丽参赛的概率.
(2)你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读探索
问题背景:著名数学家华罗庚提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次”谈话“的语言.2002年8月在北京召开的国际数学大会会标取材于我国古代数学家赵爽的《勾股圆方图注》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图1所示).勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积进行了证明.
赵爽证明方法如下:
以a、b为直角边(b>a),以c为斜边作四个全等的直角三角形,则每个直角三角形的面积等于![]() ,把这四个直角三角形拼成如图1所示形状.
,把这四个直角三角形拼成如图1所示形状.
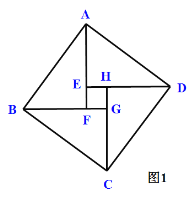
∵Rt△DAE≌Rt△ABF
∴∠EDA=∠FAB
∵∠EAD+∠EDA=90°
∴∠FAB+∠EAD=90°
∴四边形ABCD是一个边长为c的正方形,它的面积等于![]()
∵EF=FG=GH=HE=b-a
∠HEF=90°
∴四边形EFGH是一个边长为b-a的正方形,它的面积等于![]()
∴![]()
∴![]() 从而证明了勾股定理.
从而证明了勾股定理.
思维拓展:
1、如果大正方形的面积为13,小正方形的面积为1,直角三角形的较短直角边长为a,较长直角边长为b,那么![]() 的值为 .
的值为 .
2、美国第二十届总统加菲尔德也曾经给出了勾股定理的一种证明方法,如图2所示,
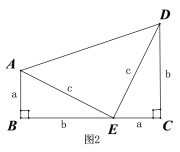
他用两个全等的直角三角形和一个等腰直角三角形拼出了一个直角梯形,请你利用此图形验证勾股定理.
证明:∵直角梯形ABCD的面积可以用两种方法表示:
第一种方法表示为:
第二种方法表示为:
∴ =
∴![]()
探索创新:
用纸做成四个全等的直角三角形,两直角边的长分别为a和b,斜边长为c,请你开动脑筋,将它们拼成一个能证明勾股定理的图形(不同于上面图1和图2).请画出你拼成的图形,并用你画的图形证明勾股定理.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,有一圆柱,其高为12cm,它的底面半径为3cm,在圆柱下底面A处有一只蚂蚁,它想得到上面B处的食物,则蚂蚁经过的最短距离为_________.(π取3)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与y轴相交于点C(0,6),与直线OA相交于点A且点A的纵坐标为2, 动点P沿路线![]() 运动.
运动.
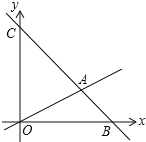
(1)求直线BC的解析式;
(2)在y轴上找一点M,使得△MAB的周长最小,则点M的坐标为______;(请直接写出结果)
(3)当△OPC的面积是△OAC的面积的![]() 时,求出这时P的坐标.
时,求出这时P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com