
科目: 来源: 题型:
【题目】法国数学家柯西于1813年在拉格朗日、高斯的基础上彻底证明了《费马多边形数定理》,其主要突破在“五边形数”的证明上.如图为前几个“五边形数”的对应图形,请据此推断,第10个“五边形数”应该为( ),第2018个“五边形数”的奇偶性为( )

A. 145;偶数 B. 145;奇数 C. 176;偶数 D. 176;奇数
查看答案和解析>>
科目: 来源: 题型:
【题目】在自习课上,小明拿来如下框的一道题目(原问题)和合作学习小组的同学们交流.
如图1,已知△ABC,∠ACB=90°,∠ABC=45°,分别以AB,BC为边向外作△ABD与△BCE,且DA=DB,EB=EC,∠ADB=∠BEC=90°,连接DE交AB于点F.探究线段DF与EF的数量关系.
小红同学的思路是:过点D作DG⊥AB于点G,构造全等三角形,通过推理使问题得解.
小华同学说:我做过一道类似的题目,不同的是∠ABC=30°,∠ADB=∠BEC=60°.
请你参考小明同学的思路,探究并解决以下问题:
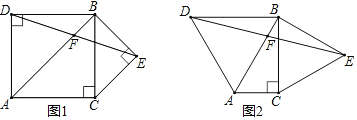
(1)写出原问题中DF与EF的数量关系为 .
(2)如图2,若∠ABC=30°,∠ADB=∠BEC=60°,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】动手操作:
如图,已知AB∥CD,点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以点E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.
问题解决:
(1)若∠ACD=78°,求∠MAB的度数;
(2)若CN⊥AM,垂足为点N,求证:△CAN≌△CMN.
实验探究:
(3)直接写出当∠CAB的度数为多少时?△CAM分别为等边三角形和等腰直角三角形.
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市在2017年“双11”,销售一批用16800元购进的中老年人保暖内衣,发现供不应求.为了备战“双12”,积极参与支付宝扫码领红包活动,超市又用36400元购进了第二批这种保暖内衣,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该超市购进的第一批保暖内衣是多少件?
(2)两批保暖内衣按相同的标价销售,最后剩下的50件按六折优惠卖出,两批保暖内衣全部售完后利润没有低于进价的20%(不考虑其他因素),请计算每件保暖内衣的标价至少是多少元?

查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,过y轴上一点A作平行于x轴的直线交某函数图象于点D,点P是x轴上一动点,连接DP,过点P作DP的垂线交y轴于点E(E在线段OA上,E不与点O重合),则称∠DPE为点D,P,E的“平横纵直角”.图1为点D,P,E的“平横纵直角”的示意图.如图2,在平面直角坐标系xOy中,已知二次函数图象与y轴交于点F(0,m),与x轴分别交于点B(﹣3,0),C(12,0).若过点F作平行于x轴的直线交抛物线于点N.

(1)点N的横坐标为 ;
(2)已知一直角为点N,M,K的“平横纵直角”,若在线段OC上存在不同的两点M1、M2,使相应的点K1、K2都与点F重合,试求m的取值范围;
(3)设抛物线的顶点为点Q,连接BQ与FN交于点H,当45°≤∠QHN≤60°时,求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠CAB=90°,F是AB边上一点,作射线CF,过点B作BG⊥CF于点G,连接AG.
(1)求证:∠ABG=∠ACF;
(2)用等式表示线段CG,AG,BG之间的等量关系,并证明.

查看答案和解析>>
科目: 来源: 题型:
【题目】阅读与思考
x2+(p+q)x+pq型式子的因式分解
x2+(p+q)x+pq型式子是数学学习中常见的一类多项式,如何将这种类型的式子分解因式呢?
我们通过学习,利用多项式的乘法法则可知:(x+p)(x+q)=x2+(p+q)x+pq,因式分解是整式乘法相反方向的变形,利用这种关系可得x2+(p+q)x+pq=(x+p)(x+q).
利用这个结果可以将某些二次项系数是1的二次三项式分解因式,例如,将x2﹣x﹣6分解因式.这个式子的二次项系数是1,常数项﹣6=2×(﹣3),一次项系数﹣1=2+(﹣3),因此这是一个x2+(p+q)x+pq型的式子.所以x2﹣x﹣6=(x+2)(x﹣3).
上述过程可用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数,如图所示.
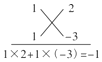
这样我们也可以得到x2﹣x﹣6=(x+2)(x﹣3).这种分解二次三项式的方法叫“十字相乘法”.
请同学们认真观察,分析理解后,解答下列问题:
(1)分解因式:y2﹣2y﹣24.
(2)若x2+mx﹣12(m为常数)可分解为两个一次因式的积,请直接写出整数m的所有可能值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=4.41cm,BC=8.83cm,P是BC上一动点,连接AP,设P,C两点间的距离为xcm,P,A两点间的距离为ycm.(当点P与点C重合时,x的值为0)小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如表:
x/cm | 0 | 0.43 | 1.00 | 1.50 | 1.85 | 2.50 | 3.60 | 4.00 | 4.30 | 5.00 | 5.50 | 6.00 | 6.62 | 7.50 | 8.00 | 8.83 |
y/cm | 7.65 | 7.28 | 6.80 | 6.39 | 6.11 | 5.62 | 4.87 |
| 4.47 | 4.15 | 3.99 | 3.87 | 3.82 | 3.92 | 4.06 | 4.41 |
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当PA=PC时,PC的长度约为 cm.(结果保留一位小数)
查看答案和解析>>
科目: 来源: 题型:
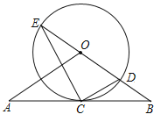
【题目】已知:如图,在△OAB中,OA=OB,⊙O经过AB的中点C,与OB交于点D,且与BO的延长线交于点E,连接EC,CD.
(1)试判断AB与⊙O的位置关系,并加以证明;
(2)若tanE=![]() ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com