
科目: 来源: 题型:
【题目】如图,直线y=kx+b经过点A(5,0),B(1,4).
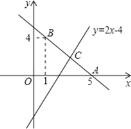
(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4≥kx+b的解集.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 开始沿折线
开始沿折线![]() 以
以![]() 的速度运动,点
的速度运动,点![]() 从
从![]() 开始沿
开始沿![]() 边以
边以![]() 的速度移动,如果点
的速度移动,如果点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,当其中一点到达
同时出发,当其中一点到达![]() 时,另一点也随之停止运动,设运动时间为
时,另一点也随之停止运动,设运动时间为![]() ,当
,当![]() ________时,四边形
________时,四边形![]() 也为矩形.
也为矩形.

查看答案和解析>>
科目: 来源: 题型:
【题目】为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式,如图描述了两种方式应支付金额y(元)与骑行时间x(时)之间的函数关系,根据图象回答下列问题:
(1)求手机支付金额y(元)与骑行时间x(时)的函数关系式;
(2)李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为(0,4),线段
的坐标为(0,4),线段![]() 的位置如图所示,其中点
的位置如图所示,其中点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点
),点![]() 的坐标为(3,
的坐标为(3,![]() ).
).

(1)将线段![]() 平移得到线段
平移得到线段![]() ,其中点
,其中点![]() 的对应点为
的对应点为![]() ,点
,点![]() 的对应点为点
的对应点为点![]() .
.
①点![]() 平移到点
平移到点![]() 的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
②点![]() 的坐标为 .
的坐标为 .
(2)在(1)的条件下,若点![]() 的坐标为(4,0),连接
的坐标为(4,0),连接![]() ,画出图形并求
,画出图形并求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】2012年“国际攀岩比赛”在重庆举行.小丽从家出发开车前去观看,途中发现忘了带门票,于是打电话让妈妈马上从家里送来,同时小丽也往回开,遇到妈妈后聊了一会儿,接着继续开车前往比赛现场.设小丽从家出发后所用时间为t,小丽与比赛现场的距离为S.下面能反映S与t的函数关系的大致图象是( )
A.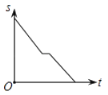 B.
B.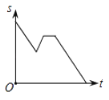 C.
C. D.
D.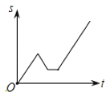
查看答案和解析>>
科目: 来源: 题型:
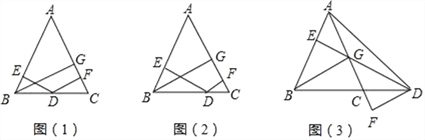
【题目】如图,在△ABC中,AB=AC,BG⊥AC于G,DE⊥AB于E,DF⊥AC于F.
(1)在图(1)中,D是BC边上的中点,判断DE+DF和BG的关系,并说明理由.
(2)在图(2)中,D是线段BC上的任意一点,DE+DF和BG的关系是否仍然成立?如果成立,证明你的结论;如果不成立,请说明理由.
(3)在图(3)中,D是线段BC延长线上的点,探究DE、DF与BG的关系.(不要求证明,直接写出结果)
查看答案和解析>>
科目: 来源: 题型:
【题目】问题探究:在边长为4的正方形ABCD中,对角线AC、BD交于点O.
探究1:如图1,若点P是对角线BD上任意一点,求线段AP的长的取值范围;
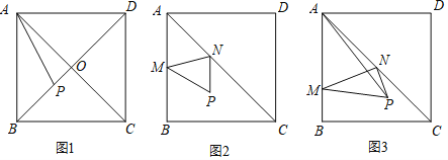
探究2:如图2,若点P是△ABC内任意一点,点M、N分别是AB边和对角线AC上的两个动点,则当AP的值在探究1中的取值范围内变化时,△PMN的周长是否存在最小值?如果存在,请求出△PMN周长的最小值,若不存在,请说明理由;
问题解决:如图3,在边长为4的正方形ABCD中,点P是△ABC内任意一点,且AP=4,点M、N分别是AB边和对角线AC上的两个动点,则当△PMN的周长取到最小值时,直接求四边形AMPN面积的最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com